Question Number 45844 by ahmadpat222@gmail.com last updated on 17/Oct/18
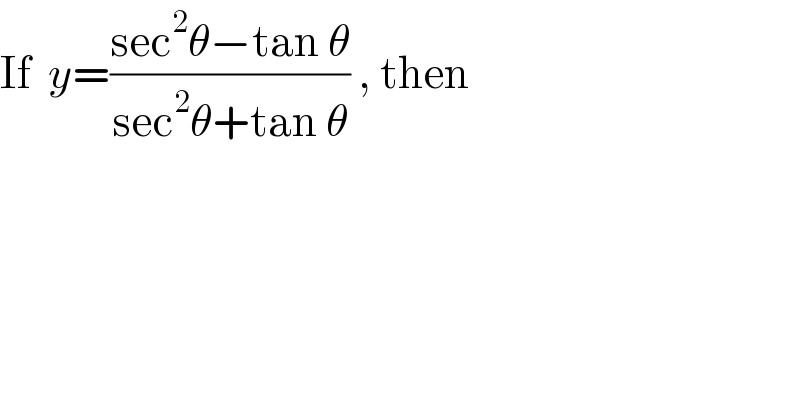
$$\mathrm{If}\:\:{y}=\frac{\mathrm{sec}^{\mathrm{2}} \theta−\mathrm{tan}\:\theta}{\mathrm{sec}^{\mathrm{2}} \theta+\mathrm{tan}\:\theta}\:,\:\mathrm{then} \\ $$
Commented by MJS last updated on 17/Oct/18
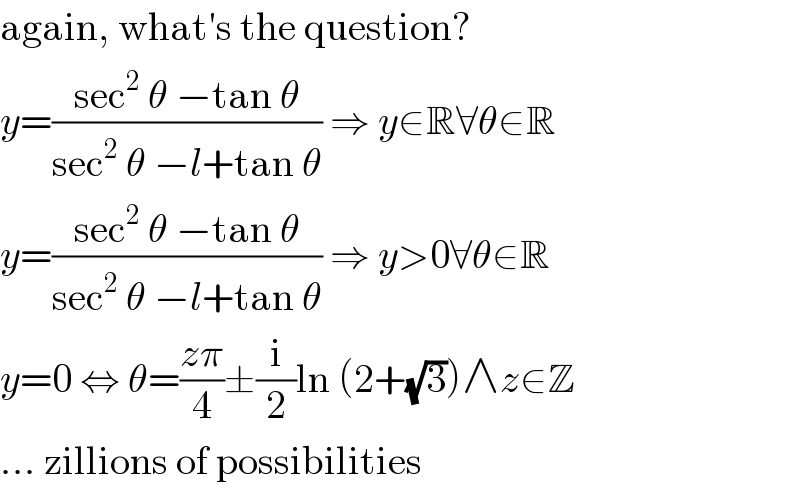
$$\mathrm{again},\:\mathrm{what}'\mathrm{s}\:\mathrm{the}\:\mathrm{question}? \\ $$$${y}=\frac{\mathrm{sec}^{\mathrm{2}} \:\theta\:−\mathrm{tan}\:\theta}{\mathrm{sec}^{\mathrm{2}} \:\theta\:−{l}+\mathrm{tan}\:\theta}\:\Rightarrow\:{y}\in\mathbb{R}\forall\theta\in\mathbb{R} \\ $$$${y}=\frac{\mathrm{sec}^{\mathrm{2}} \:\theta\:−\mathrm{tan}\:\theta}{\mathrm{sec}^{\mathrm{2}} \:\theta\:−{l}+\mathrm{tan}\:\theta}\:\Rightarrow\:{y}>\mathrm{0}\forall\theta\in\mathbb{R} \\ $$$${y}=\mathrm{0}\:\Leftrightarrow\:\theta=\frac{{z}\pi}{\mathrm{4}}\pm\frac{\mathrm{i}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\wedge{z}\in\mathbb{Z} \\ $$$$…\:\mathrm{zillions}\:\mathrm{of}\:\mathrm{possibilities} \\ $$
Answered by MJS last updated on 17/Oct/18
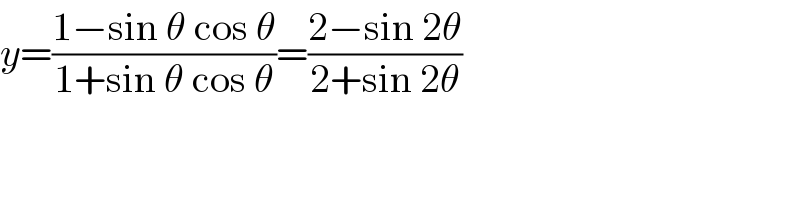
$${y}=\frac{\mathrm{1}−\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}{\mathrm{1}+\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}=\frac{\mathrm{2}−\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{2}+\mathrm{sin}\:\mathrm{2}\theta} \\ $$
