In-2x-3y-8-and-5x-Ky-3-find-the-value-of-K-so-that-the-given-system-of-equation-has-infinte-solution-

Question Number 106666 by deep last updated on 06/Aug/20

In 2 x + 3 y = 8 and 5 x + K y = 3, find the

value of K so that the given system

of equation has infinte solution .

Commented by bemath last updated on 06/Aug/20

(\begin{matrix} 2 3 \\ 5 k \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} 8 \\ 3 \end{matrix})

has no solution if Δ = 0

\Rightarrow 2 k - 15 = 0, k = \frac{15}{2}

Commented by Her_Majesty last updated on 06/Aug/20

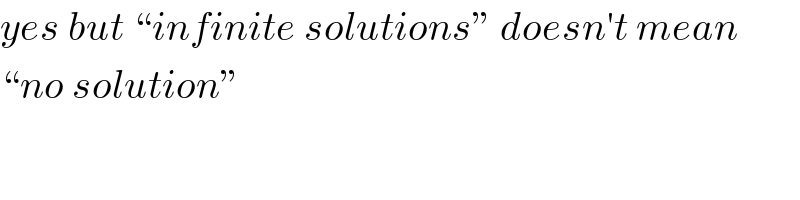
y e s b u t “ i n f i n i t e {s o l u t i o n s}^{″} {d o e s n}^{'} t m e a n

“ n o {s o l u t i o n}^{″}

Answered by nimnim last updated on 06/Aug/20

T h e e q u a t i o n s w i l l h a v e i n f i n i t e s o l u t i o n i f

\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}} i . e \frac{2}{5} = \frac{3}{k} = \frac{8}{3} \Rightarrow 1 = \frac{5}{3} \times \frac{3}{k} \times \frac{3}{8} = 1

\Rightarrow 1 = \frac{15}{8 k} = 1 \Rightarrow k = \frac{15}{8}

Commented by Her_Majesty last updated on 06/Aug/20

w r o n g . w i t h k = \frac{15}{8} w e g e t x = - \frac{8}{15} \land y = \frac{136}{45}

w h i c h i s a u n i q u e s o l u t i o n

Answered by Her_Majesty last updated on 06/Aug/20

{\begin{cases} 2 x + 3 y = 8 \\ 5 x + K y = 3 \end{cases} \Leftrightarrow {\begin{cases} y = - \frac{2}{3} x + \frac{8}{3} \\ y = - \frac{5}{k} x + \frac{3}{k} \end{cases}

b o t h a r e l i n e a r \Rightarrow i n f i n i t e s o l u t i o n s i f

(I) = (I I) w h i c h i s i m p o s s i b l e i f K \in C :

>

- \frac{2}{3} = - \frac{5}{K} \land \frac{8}{3} = \frac{3}{K}

K = \frac{15}{2} \land K = \frac{9}{8} w h i c h i s i m p o s s i b l e

i f K i s n o t a n u m b e r

- \frac{2}{3} x + \frac{8}{3} = - \frac{5}{K} x + \frac{3}{K}

\Rightarrow

K = \frac{3 (5 x - 3)}{2 (x - 4)}

\Rightarrow

{\begin{cases} y = - \frac{2}{3} x + \frac{8}{3} \\ y = - \frac{2}{3} x + \frac{8}{3} \end{cases}