Question Number 113848 by deepraj123 last updated on 15/Sep/20
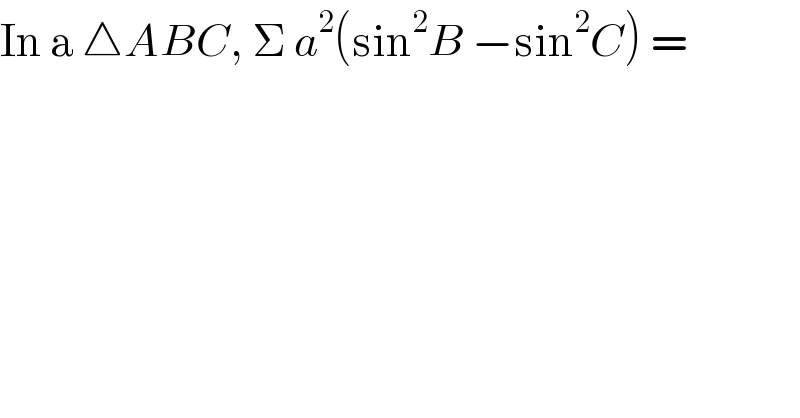
$$\mathrm{In}\:\mathrm{a}\:\bigtriangleup{ABC},\:\Sigma\:{a}^{\mathrm{2}} \left(\mathrm{sin}^{\mathrm{2}} {B}\:−\mathrm{sin}^{\mathrm{2}} {C}\right)\:= \\ $$
Answered by 1549442205PVT last updated on 16/Sep/20
![We have Σa^2 (sin^2 B−sin^2 C)= a^2 (sin^2 B−sin^2 C )+b^2 (sin^2 C−sin^2 A) +c^2 (sin^2 A−sin^2 B) From sine theorem we have: (a/(sinA))=(b/(sinB))=(c/(sinC))=2R⇒a^2 =4R^2 sin^2 A b^2 =4R^2 sin^2 B,c^2 =4R^2 sim^2 C.Replace into above equality we get Σa^2 (sin^2 B−sin^2 C) =4R^2 [sin^2 A(sin^2 B−sin^2 C)+sin^2 B(sin^2 C−sin^2 A) +sin^2 C(sin^2 A−sin^2 B)]. (Put x=sin^2 A,y=sin^2 B,z=sin^2 C ) =4R^2 [x(y−z)+y(z−x)+z(x−y)] =4R^2 (xy−xz+yz−yx+zx−zy)=0](https://www.tinkutara.com/question/Q113955.png)
$$\mathrm{We}\:\mathrm{have}\:\Sigma\mathrm{a}^{\mathrm{2}} \left(\mathrm{sin}^{\mathrm{2}} \mathrm{B}−\mathrm{sin}^{\mathrm{2}} \mathrm{C}\right)= \\ $$$$\mathrm{a}^{\mathrm{2}} \left(\mathrm{sin}^{\mathrm{2}} \mathrm{B}−\mathrm{sin}^{\mathrm{2}} \mathrm{C}\:\right)+\mathrm{b}^{\mathrm{2}} \left(\mathrm{sin}^{\mathrm{2}} \mathrm{C}−\mathrm{sin}^{\mathrm{2}} \mathrm{A}\right) \\ $$$$+\mathrm{c}^{\mathrm{2}} \left(\mathrm{sin}^{\mathrm{2}} \mathrm{A}−\mathrm{sin}^{\mathrm{2}} \mathrm{B}\right) \\ $$$$\mathrm{From}\:\mathrm{sine}\:\mathrm{theorem}\:\mathrm{we}\:\mathrm{have}: \\ $$$$\frac{\mathrm{a}}{\mathrm{sinA}}=\frac{\mathrm{b}}{\mathrm{sinB}}=\frac{\mathrm{c}}{\mathrm{sinC}}=\mathrm{2R}\Rightarrow\mathrm{a}^{\mathrm{2}} =\mathrm{4R}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \mathrm{A} \\ $$$$\mathrm{b}^{\mathrm{2}} =\mathrm{4R}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \mathrm{B},\mathrm{c}^{\mathrm{2}} =\mathrm{4R}^{\mathrm{2}} \mathrm{sim}^{\mathrm{2}} \mathrm{C}.\mathrm{Replace}\:\mathrm{into} \\ $$$$\mathrm{above}\:\mathrm{equality}\:\mathrm{we}\:\mathrm{get}\:\Sigma\mathrm{a}^{\mathrm{2}} \left(\mathrm{sin}^{\mathrm{2}} \mathrm{B}−\mathrm{sin}^{\mathrm{2}} \mathrm{C}\right) \\ $$$$=\mathrm{4R}^{\mathrm{2}} \left[\mathrm{sin}^{\mathrm{2}} \mathrm{A}\left(\mathrm{sin}^{\mathrm{2}} \mathrm{B}−\mathrm{sin}^{\mathrm{2}} \mathrm{C}\right)+\mathrm{sin}^{\mathrm{2}} \mathrm{B}\left(\mathrm{sin}^{\mathrm{2}} \mathrm{C}−\mathrm{sin}^{\mathrm{2}} \mathrm{A}\right)\right. \\ $$$$\left.+\mathrm{sin}^{\mathrm{2}} \mathrm{C}\left(\mathrm{sin}^{\mathrm{2}} \mathrm{A}−\mathrm{sin}^{\mathrm{2}} \mathrm{B}\right)\right]. \\ $$$$\left(\mathrm{Put}\:\mathrm{x}=\mathrm{sin}^{\mathrm{2}} \mathrm{A},\mathrm{y}=\mathrm{sin}^{\mathrm{2}} \mathrm{B},\mathrm{z}=\mathrm{sin}^{\mathrm{2}} \mathrm{C}\:\right) \\ $$$$=\mathrm{4R}^{\mathrm{2}} \left[\mathrm{x}\left(\mathrm{y}−\mathrm{z}\right)+\mathrm{y}\left(\mathrm{z}−\mathrm{x}\right)+\mathrm{z}\left(\mathrm{x}−\mathrm{y}\right)\right] \\ $$$$=\mathrm{4R}^{\mathrm{2}} \left(\mathrm{xy}−\mathrm{xz}+\mathrm{yz}−\mathrm{yx}+\mathrm{zx}−\mathrm{zy}\right)=\mathrm{0} \\ $$
