Question Number 44034 by Dilshad786 last updated on 20/Sep/18
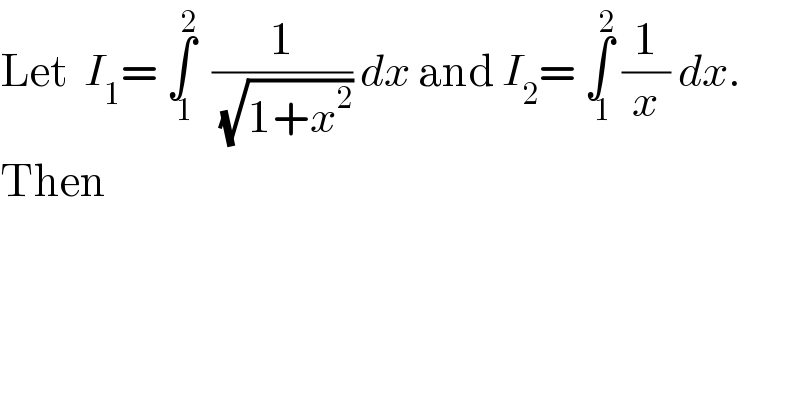
$$\mathrm{Let}\:\:{I}_{\mathrm{1}} =\:\underset{\:\mathrm{1}} {\overset{\mathrm{2}} {\int}}\:\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:{dx}\:\mathrm{and}\:{I}_{\mathrm{2}} =\:\underset{\:\mathrm{1}} {\overset{\mathrm{2}} {\int}}\:\frac{\mathrm{1}}{{x}}\:{dx}. \\ $$$$\mathrm{Then} \\ $$
Commented by maxmathsup by imad last updated on 20/Sep/18
![I_1 =[ln(x+(√(1+x^2 ))]_1 ^2 =ln(2+(√5))−ln(1+(√2)) and I_2 =[ln∣x∣]_1 ^2 =ln(2) .](https://www.tinkutara.com/question/Q44043.png)
$${I}_{\mathrm{1}} =\left[{ln}\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right]_{\mathrm{1}} ^{\mathrm{2}} \:={ln}\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)−{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\:\:{and}\:\right. \\ $$$${I}_{\mathrm{2}} =\left[{ln}\mid{x}\mid\right]_{\mathrm{1}} ^{\mathrm{2}} ={ln}\left(\mathrm{2}\right)\:. \\ $$
