Question Number 53696 by gunawan last updated on 25/Jan/19
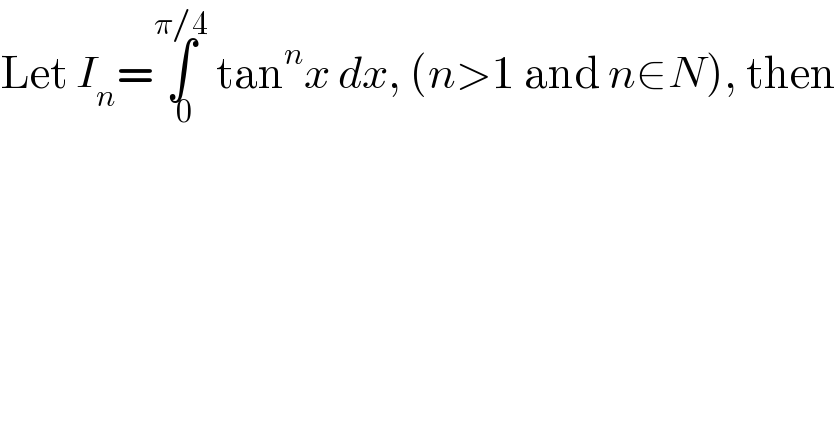
$$\mathrm{Let}\:{I}_{{n}} =\underset{\:\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\:\mathrm{tan}^{{n}} {x}\:{dx},\:\left({n}>\mathrm{1}\:\mathrm{and}\:{n}\in{N}\right),\:\mathrm{then} \\ $$
Commented by Abdo msup. last updated on 25/Jan/19
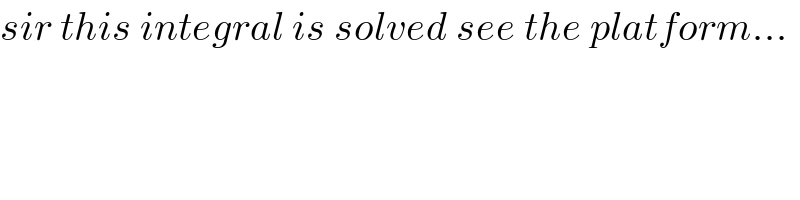
$${sir}\:{this}\:{integral}\:{is}\:{solved}\:{see}\:{the}\:{platform}… \\ $$
Commented by gunawan last updated on 25/Jan/19

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{Sir} \\ $$$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{this}\:\mathrm{integral}\:\mathrm{is}\:\mathrm{solved} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 25/Jan/19

$${J}_{{n}} =\int{tan}^{{n}−\mathrm{2}} {xtan}^{\mathrm{2}} {xdx} \\ $$$${j}_{{n}} .=\int{tan}^{{n}−\mathrm{2}} {x}\left({sec}^{\mathrm{2}} {x}−\mathrm{1}\right){dx} \\ $$$$=\int{tan}^{{n}−\mathrm{2}} {xd}\left({tanx}\right)−\int{tan}^{{n}−\mathrm{2}} {xdx} \\ $$$${j}_{{n}} =\frac{\left({tan}^{{n}−\mathrm{2}+\mathrm{1}} {x}\right)}{{n}−\mathrm{2}+\mathrm{1}}−{j}_{{n}−\mathrm{2}} \\ $$$${so} \\ $$$${I}_{{n}} =\mid\frac{{tan}^{{n}−\mathrm{1}} {x}}{{n}−\mathrm{1}}\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} −{I}_{{n}−\mathrm{2}} \\ $$$${I}_{{n}} =\frac{\mathrm{1}}{{n}−\mathrm{1}}−{I}_{{n}−\mathrm{2}} \leftarrow{reduction}\:{formula} \\ $$$${I}_{{n}−\mathrm{2}} =\frac{\mathrm{1}}{{n}−\mathrm{3}}−{I}_{{n}−\mathrm{4}} \\ $$$${I}_{{n}−\mathrm{4}} =\frac{\mathrm{1}}{{n}−\mathrm{5}\:}−{I}_{{n}−\mathrm{6}\:} \\ $$$$….. \\ $$$$….. \\ $$$${I}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}−\mathrm{1}}−{I}_{\mathrm{0}} \\ $$$$\:\:\:{now}\:{I}_{\mathrm{0}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left({tanx}\right)^{\mathrm{0}} {dx}=\mid{x}\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} =\frac{\pi}{\mathrm{4}} \\ $$$${now}\:{I}_{\mathrm{2}} .=\frac{\mathrm{1}}{\mathrm{2}−\mathrm{1}}−\frac{\pi}{\mathrm{4}}.=\frac{\mathrm{1}}{\mathrm{1}}−\frac{\pi}{\mathrm{4}} \\ $$$$ \\ $$$$ \\ $$
Commented by peter frank last updated on 25/Jan/19
$${nice}\:{work}\:{sir} \\ $$
Answered by peter frank last updated on 25/Jan/19
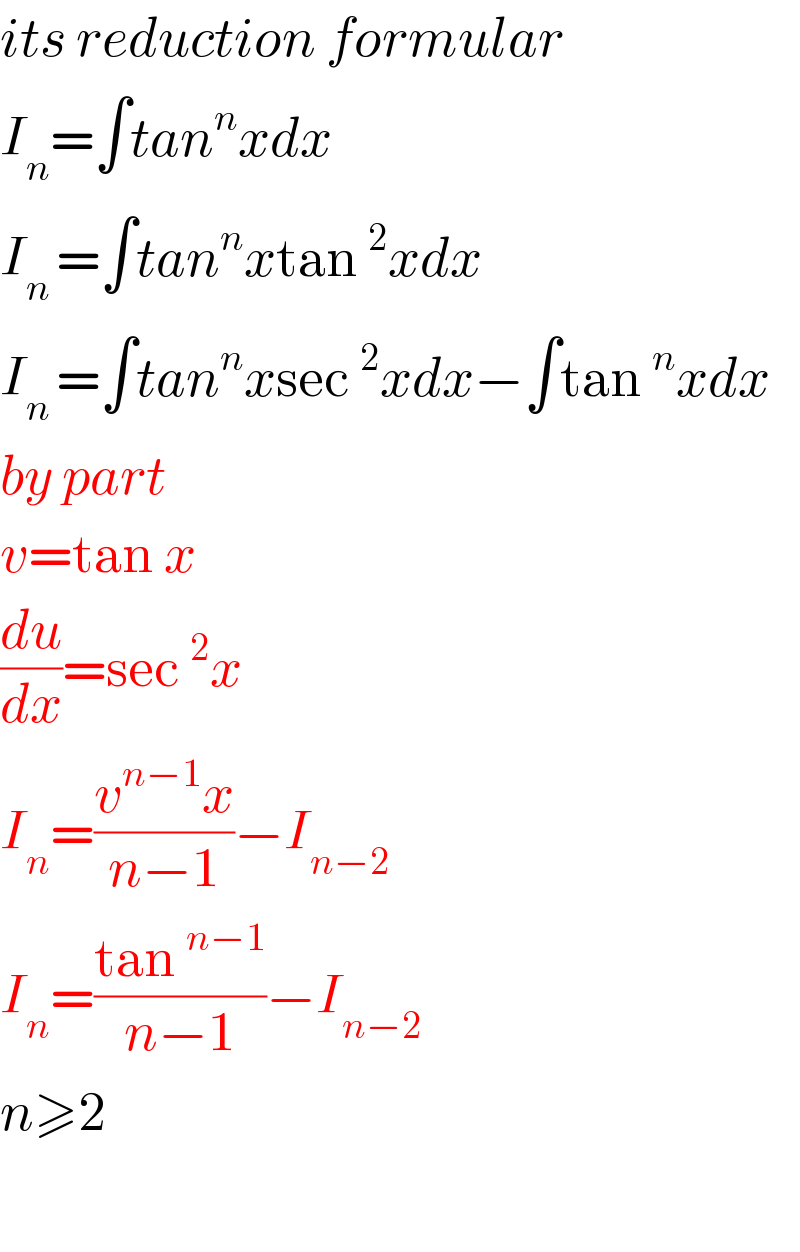
$${its}\:{reduction}\:{formular} \\ $$$${I}_{{n}} =\int{tan}^{{n}} {xdx} \\ $$$${I}_{{n}\:} =\int{tan}^{{n}} {x}\mathrm{tan}\:^{\mathrm{2}} {xdx} \\ $$$${I}_{{n}\:} =\int{tan}^{{n}} {x}\mathrm{sec}\:^{\mathrm{2}} {xdx}−\int\mathrm{tan}\:^{{n}} {xdx} \\ $$$${by}\:{part} \\ $$$${v}=\mathrm{tan}\:{x} \\ $$$$\frac{{du}}{{dx}}=\mathrm{sec}\:^{\mathrm{2}} {x} \\ $$$${I}_{{n}} =\frac{{v}^{{n}−\mathrm{1}} {x}}{{n}−\mathrm{1}}−{I}_{{n}−\mathrm{2}} \\ $$$${I}_{{n}} =\frac{\mathrm{tan}\:^{{n}−\mathrm{1}} }{{n}−\mathrm{1}}−{I}_{{n}−\mathrm{2}} \\ $$$${n}\geqslant\mathrm{2} \\ $$$$ \\ $$
