Question Number 27203 by julli deswal last updated on 03/Jan/18
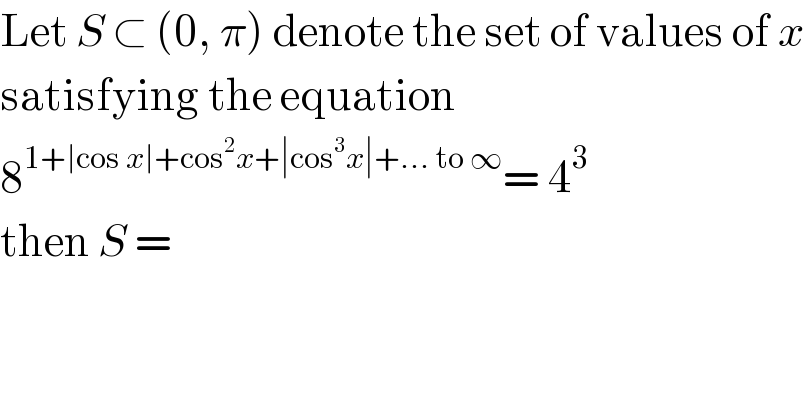
$$\mathrm{Let}\:{S}\:\subset\:\left(\mathrm{0},\:\pi\right)\:\mathrm{denote}\:\mathrm{the}\:\mathrm{set}\:\mathrm{of}\:\mathrm{values}\:\mathrm{of}\:{x} \\ $$$$\mathrm{satisfying}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{8}^{\mathrm{1}+\mid\mathrm{cos}\:{x}\mid+\mathrm{cos}^{\mathrm{2}} {x}+\mid\mathrm{cos}^{\mathrm{3}} {x}\mid+…\:\mathrm{to}\:\infty} =\:\mathrm{4}^{\mathrm{3}} \\ $$$$\mathrm{then}\:{S}\:=\: \\ $$
Answered by Tinkutara last updated on 03/Jan/18
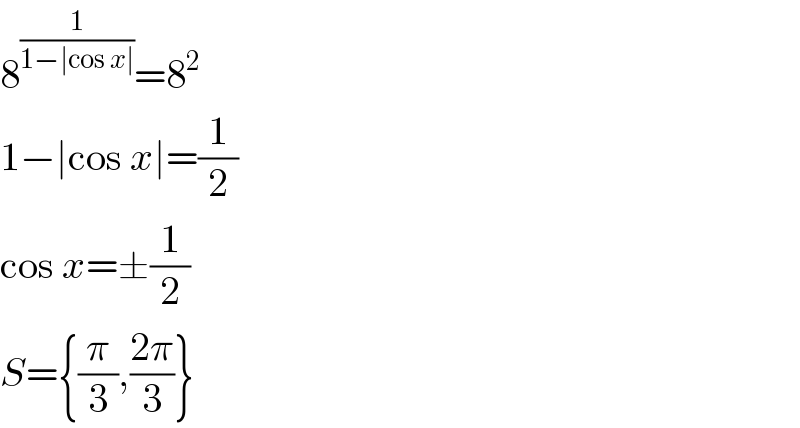
$$\mathrm{8}^{\frac{\mathrm{1}}{\mathrm{1}−\mid\mathrm{cos}\:{x}\mid}} =\mathrm{8}^{\mathrm{2}} \\ $$$$\mathrm{1}−\mid\mathrm{cos}\:{x}\mid=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{cos}\:{x}=\pm\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${S}=\left\{\frac{\pi}{\mathrm{3}},\frac{\mathrm{2}\pi}{\mathrm{3}}\right\} \\ $$
Answered by mrW1 last updated on 03/Jan/18
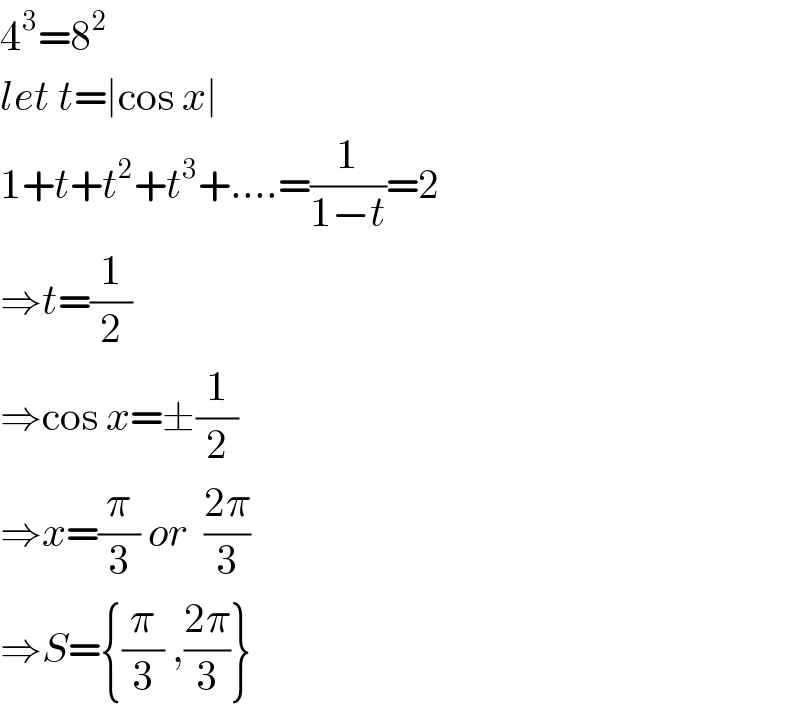
$$\mathrm{4}^{\mathrm{3}} =\mathrm{8}^{\mathrm{2}} \\ $$$${let}\:{t}=\mid\mathrm{cos}\:{x}\mid \\ $$$$\mathrm{1}+{t}+{t}^{\mathrm{2}} +{t}^{\mathrm{3}} +….=\frac{\mathrm{1}}{\mathrm{1}−{t}}=\mathrm{2} \\ $$$$\Rightarrow{t}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{cos}\:{x}=\pm\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{x}=\frac{\pi}{\mathrm{3}}\:{or}\:\:\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\Rightarrow{S}=\left\{\frac{\pi}{\mathrm{3}}\:,\frac{\mathrm{2}\pi}{\mathrm{3}}\right\} \\ $$
