Question Number 27604 by 0722136841 last updated on 10/Jan/18
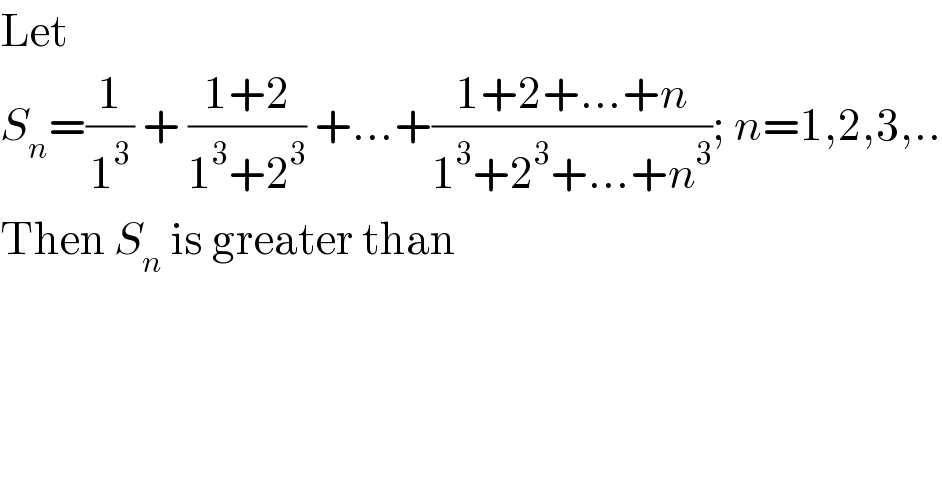
$$\mathrm{Let}\: \\ $$$${S}_{{n}} =\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{3}} }\:+\:\frac{\mathrm{1}+\mathrm{2}}{\mathrm{1}^{\mathrm{3}} +\mathrm{2}^{\mathrm{3}} }\:+…+\frac{\mathrm{1}+\mathrm{2}+…+{n}}{\mathrm{1}^{\mathrm{3}} +\mathrm{2}^{\mathrm{3}} +…+{n}^{\mathrm{3}} };\:{n}=\mathrm{1},\mathrm{2},\mathrm{3},.. \\ $$$$\mathrm{Then}\:{S}_{{n}} \:\mathrm{is}\:\mathrm{greater}\:\mathrm{than} \\ $$
Commented by abdo imad last updated on 11/Jan/18
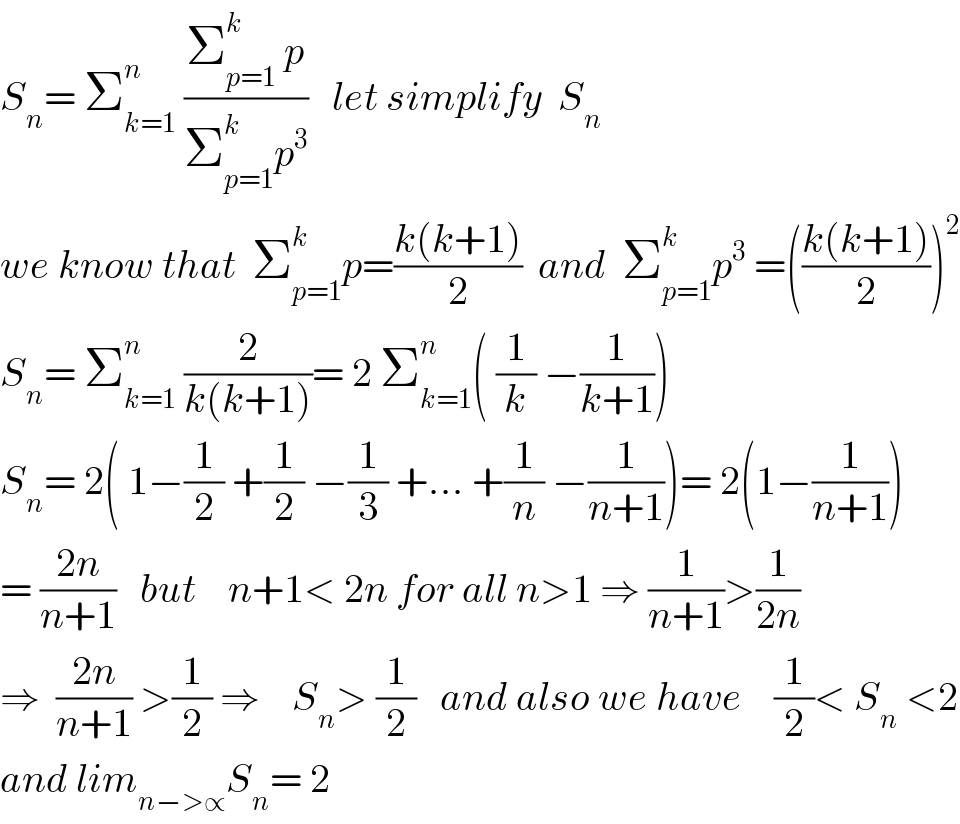
$${S}_{{n}} =\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\sum_{{p}=\mathrm{1}} ^{{k}} \:{p}}{\sum_{{p}=\mathrm{1}} ^{{k}} {p}^{\mathrm{3}} }\:\:\:{let}\:{simplify}\:\:{S}_{{n}} \\ $$$${we}\:{know}\:{that}\:\:\sum_{{p}=\mathrm{1}} ^{{k}} {p}=\frac{{k}\left({k}+\mathrm{1}\right)}{\mathrm{2}}\:\:{and}\:\:\sum_{{p}=\mathrm{1}} ^{{k}} {p}^{\mathrm{3}} \:=\left(\frac{{k}\left({k}+\mathrm{1}\right)}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$${S}_{{n}} =\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{2}}{{k}\left({k}+\mathrm{1}\right)}=\:\mathrm{2}\:\sum_{{k}=\mathrm{1}} ^{{n}} \left(\:\frac{\mathrm{1}}{{k}}\:−\frac{\mathrm{1}}{{k}+\mathrm{1}}\right) \\ $$$${S}_{{n}} =\:\mathrm{2}\left(\:\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{3}}\:+…\:+\frac{\mathrm{1}}{{n}}\:−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right)=\:\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right) \\ $$$$=\:\frac{\mathrm{2}{n}}{{n}+\mathrm{1}}\:\:\:{but}\:\:\:\:{n}+\mathrm{1}<\:\mathrm{2}{n}\:{for}\:{all}\:{n}>\mathrm{1}\:\Rightarrow\:\frac{\mathrm{1}}{{n}+\mathrm{1}}>\frac{\mathrm{1}}{\mathrm{2}{n}} \\ $$$$\Rightarrow\:\:\frac{\mathrm{2}{n}}{{n}+\mathrm{1}}\:>\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:\:\:\:{S}_{{n}} >\:\frac{\mathrm{1}}{\mathrm{2}}\:\:\:{and}\:{also}\:{we}\:{have}\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}<\:{S}_{{n}} \:<\mathrm{2} \\ $$$${and}\:{lim}_{{n}−>\propto} {S}_{{n}} =\:\mathrm{2} \\ $$
