Question Number 55776 by gunawan last updated on 04/Mar/19
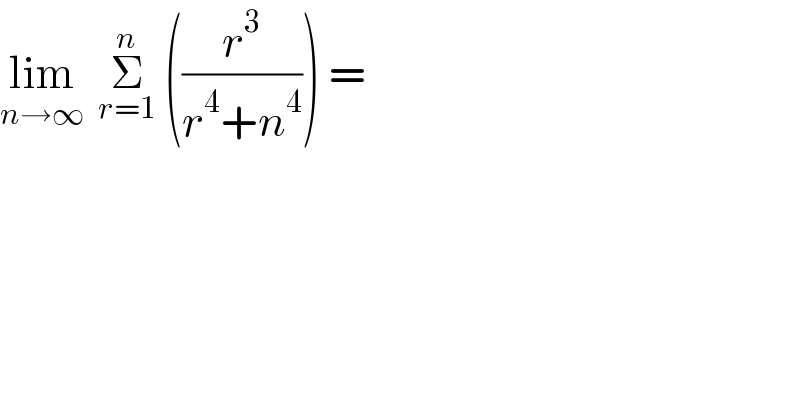
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\:\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\:\left(\frac{{r}^{\mathrm{3}} }{{r}^{\mathrm{4}} +{n}^{\mathrm{4}} }\right)\:= \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Mar/19
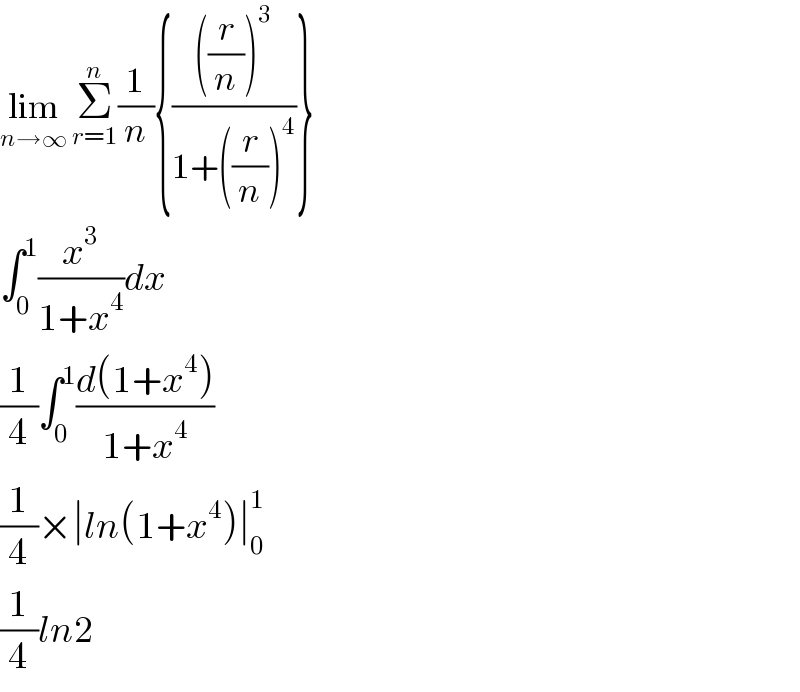
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{n}}\left\{\frac{\left(\frac{{r}}{{n}}\right)^{\mathrm{3}} }{\mathrm{1}+\left(\frac{{r}}{{n}}\right)^{\mathrm{4}} }\right\} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{3}} }{\mathrm{1}+{x}^{\mathrm{4}} }{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{d}\left(\mathrm{1}+{x}^{\mathrm{4}} \right)}{\mathrm{1}+{x}^{\mathrm{4}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}×\mid{ln}\left(\mathrm{1}+{x}^{\mathrm{4}} \right)\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}{ln}\mathrm{2} \\ $$
