Question Number 54378 by ngo last updated on 02/Feb/19
![∫_(π/3) ^(3π/2) [ 2 cos x ] dx =](https://www.tinkutara.com/question/Q54378.png)
$$\underset{\pi/\mathrm{3}} {\overset{\mathrm{3}\pi/\mathrm{2}} {\int}}\:\:\left[\:\mathrm{2}\:\mathrm{cos}\:{x}\:\right]\:{dx}\:= \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 03/Feb/19
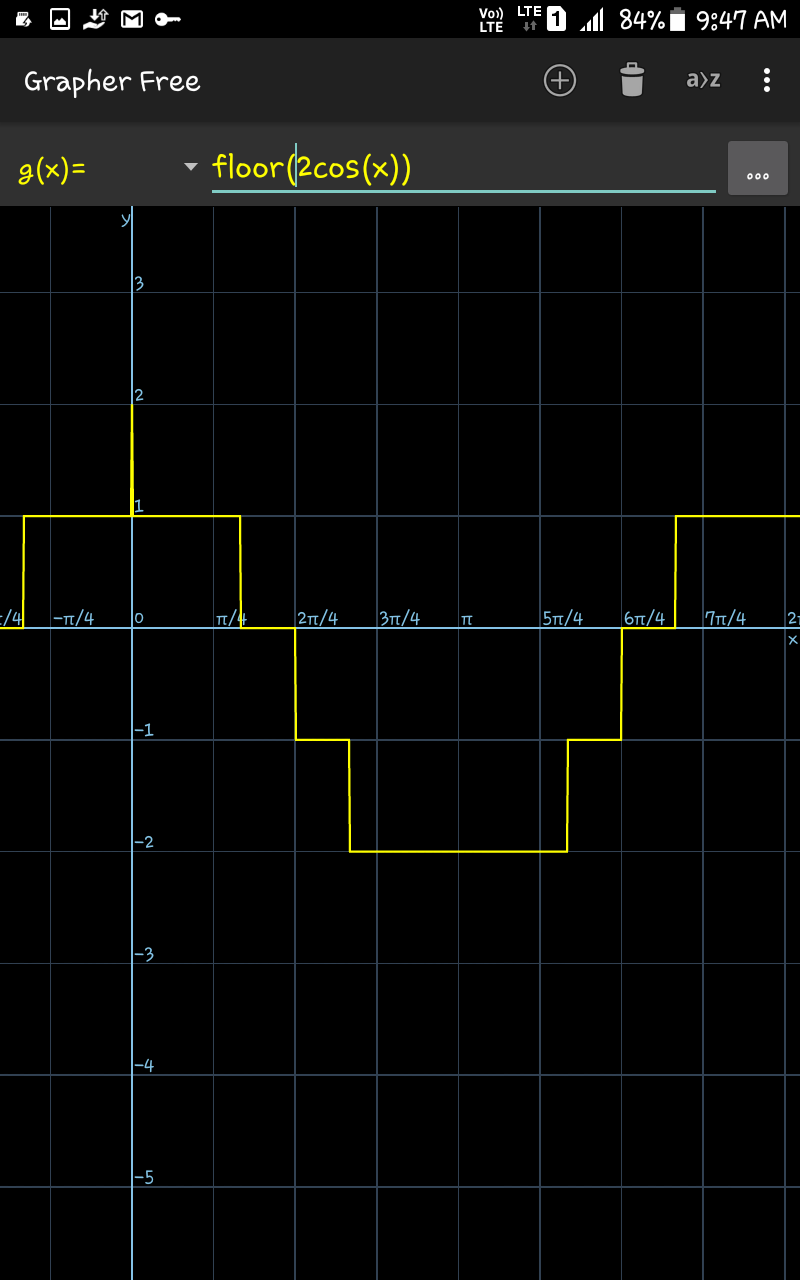
Commented by tanmay.chaudhury50@gmail.com last updated on 03/Feb/19
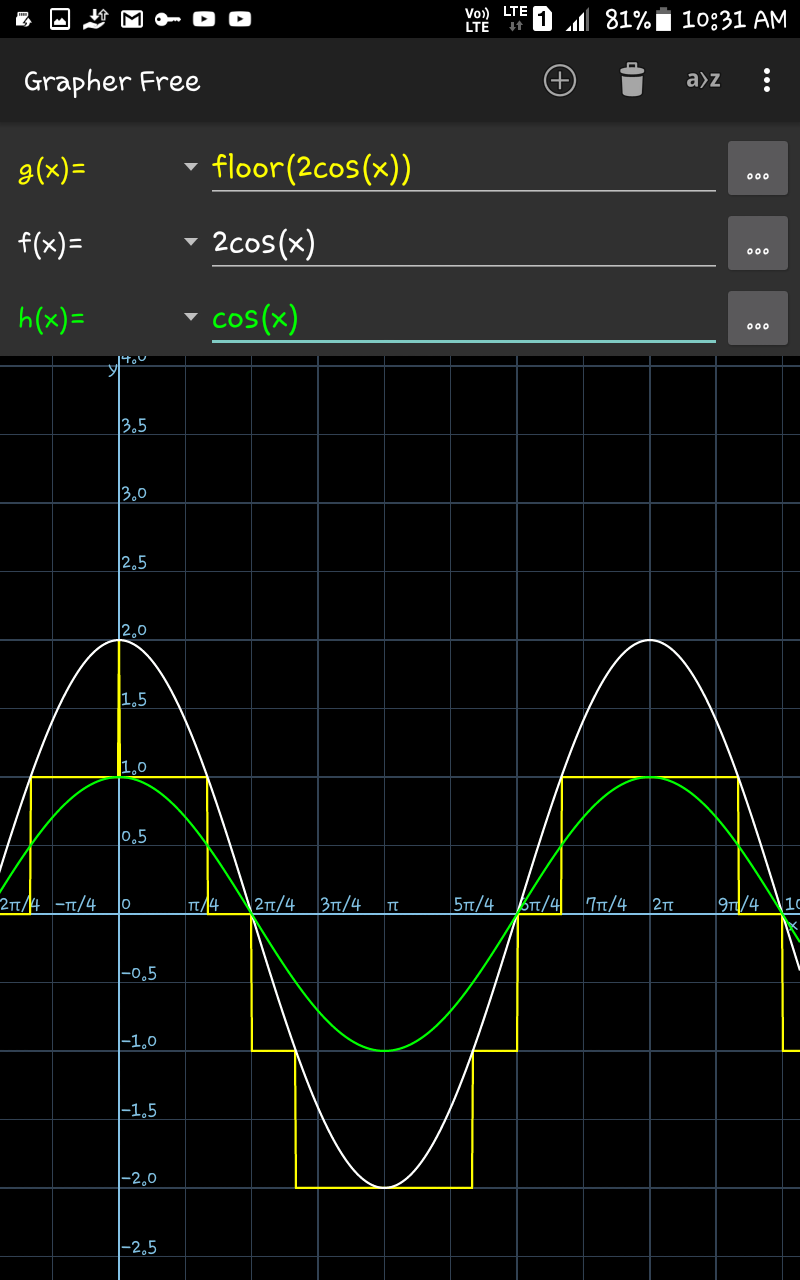
Commented by tanmay.chaudhury50@gmail.com last updated on 03/Feb/19
![with the help of graph trying to solve... ∫_(π/3) ^(π/2) [2cosx]dx+∫_(π/2) ^((2π)/3) [2cosx]dx+∫_((2π)/3) ^((4π)/3) [2cosx]dx+∫_((4π)/3) ^((3π)/2) [2cosx]dx =0+(−1)(((2π)/3)−(π/2))+(−2)(((4π)/3)−((2π)/3))+(−1)(((3π)/2)−((4π)/3)) =(−1)((π/6))+(−2)(((2π)/3))+(−1)((π/6)) =−(π/3)−((4π)/3)=((−5π)/3) pls check....](https://www.tinkutara.com/question/Q54392.png)
$${with}\:{the}\:{help}\:{of}\:{graph}\:{trying}\:{to}\:{solve}… \\ $$$$\int_{\frac{\pi}{\mathrm{3}}} ^{\frac{\pi}{\mathrm{2}}} \:\left[\mathrm{2}{cosx}\right]{dx}+\int_{\frac{\pi}{\mathrm{2}}} ^{\frac{\mathrm{2}\pi}{\mathrm{3}}} \left[\mathrm{2}{cosx}\right]{dx}+\int_{\frac{\mathrm{2}\pi}{\mathrm{3}}} ^{\frac{\mathrm{4}\pi}{\mathrm{3}}} \left[\mathrm{2}{cosx}\right]{dx}+\int_{\frac{\mathrm{4}\pi}{\mathrm{3}}} ^{\frac{\mathrm{3}\pi}{\mathrm{2}}} \:\left[\mathrm{2}{cosx}\right]{dx} \\ $$$$=\mathrm{0}+\left(−\mathrm{1}\right)\left(\frac{\mathrm{2}\pi}{\mathrm{3}}−\frac{\pi}{\mathrm{2}}\right)+\left(−\mathrm{2}\right)\left(\frac{\mathrm{4}\pi}{\mathrm{3}}−\frac{\mathrm{2}\pi}{\mathrm{3}}\right)+\left(−\mathrm{1}\right)\left(\frac{\mathrm{3}\pi}{\mathrm{2}}−\frac{\mathrm{4}\pi}{\mathrm{3}}\right) \\ $$$$=\left(−\mathrm{1}\right)\left(\frac{\pi}{\mathrm{6}}\right)+\left(−\mathrm{2}\right)\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)+\left(−\mathrm{1}\right)\left(\frac{\pi}{\mathrm{6}}\right) \\ $$$$=−\frac{\pi}{\mathrm{3}}−\frac{\mathrm{4}\pi}{\mathrm{3}}=\frac{−\mathrm{5}\pi}{\mathrm{3}} \\ $$$${pls}\:{check}…. \\ $$$$ \\ $$$$ \\ $$
