Question Number 64332 by Chi Mes Try last updated on 16/Jul/19
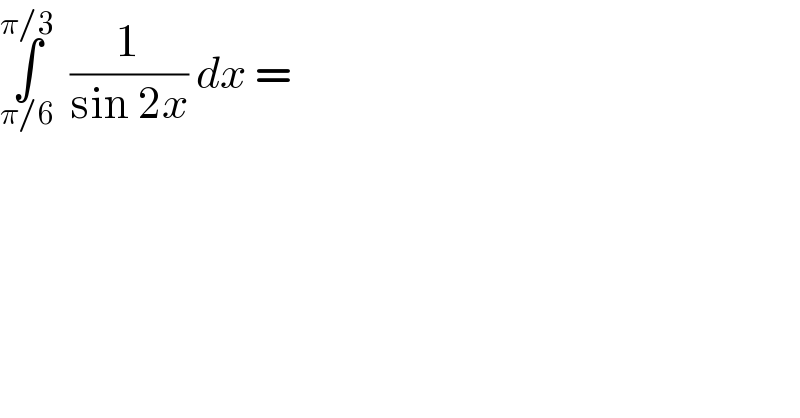
$$\underset{\pi/\mathrm{6}} {\overset{\pi/\mathrm{3}} {\int}}\:\:\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{2}{x}}\:{dx}\:= \\ $$
Commented by mathmax by abdo last updated on 16/Jul/19
![let A =∫_(π/6) ^(π/3) (dx/(sin(2x))) changement 2x=t give A =∫_(π/3) ^((2π)/3) (dt/(2sint)) =_(tan((t/2))=u) (1/2) ∫_(1/( (√3))) ^(√3) ((2du)/((1+u^2 )((2u)/(1+u^2 )))) =(1/2) ∫_(1/( (√3))) ^(√3) (du/u) =(1/2)[ln∣u∣]_(1/( (√3))) ^(√3) =(1/2){ln((√3))+ln((√3))} =((ln(3))/2) A =((ln(3))/2) .](https://www.tinkutara.com/question/Q64344.png)
$${let}\:{A}\:=\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \:\frac{{dx}}{{sin}\left(\mathrm{2}{x}\right)}\:{changement}\:\mathrm{2}{x}={t}\:{give}\: \\ $$$${A}\:=\int_{\frac{\pi}{\mathrm{3}}} ^{\frac{\mathrm{2}\pi}{\mathrm{3}}} \:\:\:\frac{{dt}}{\mathrm{2}{sint}}\:=_{{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u}} \:\:\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\sqrt{\mathrm{3}}} \:\:\:\frac{\mathrm{2}{du}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\sqrt{\mathrm{3}}} \:\frac{{du}}{{u}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[{ln}\mid{u}\mid\right]_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\sqrt{\mathrm{3}}} \:\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{{ln}\left(\sqrt{\mathrm{3}}\right)+{ln}\left(\sqrt{\mathrm{3}}\right)\right\}\:=\frac{{ln}\left(\mathrm{3}\right)}{\mathrm{2}} \\ $$$${A}\:=\frac{{ln}\left(\mathrm{3}\right)}{\mathrm{2}}\:. \\ $$
Commented by Tony Lin last updated on 17/Jul/19

$$\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \frac{\mathrm{1}}{{sin}\mathrm{2}{x}}{dx} \\ $$$$=\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} {csc}\mathrm{2}{xdx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{csc}\mathrm{2}{x}+{cot}\mathrm{2}{x}\mid\mid_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{cotx}\mid_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \\ $$$$=−\frac{{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)}{\mathrm{2}}+\frac{{ln}\left(\sqrt{\mathrm{3}}\right)}{\mathrm{2}} \\ $$$$=\frac{{ln}\mathrm{3}}{\mathrm{2}} \\ $$
