Question Number 18731 by juniorjoseph679@gmail.com last updated on 29/Jul/17
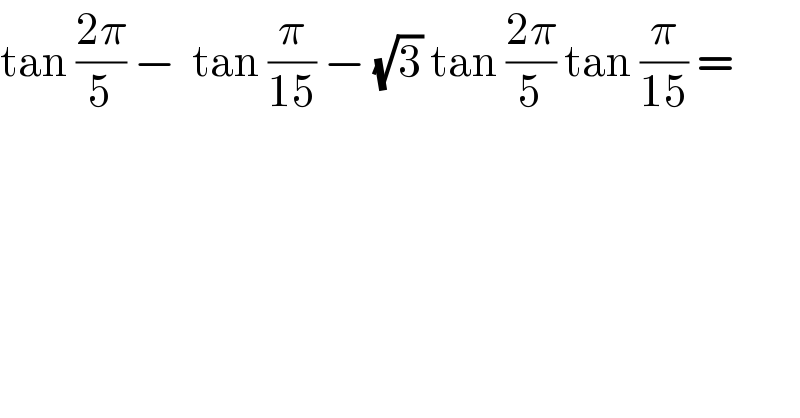
$$\mathrm{tan}\:\frac{\mathrm{2}\pi}{\mathrm{5}}\:−\:\:\mathrm{tan}\:\frac{\pi}{\mathrm{15}}\:−\:\sqrt{\mathrm{3}}\:\mathrm{tan}\:\frac{\mathrm{2}\pi}{\mathrm{5}}\:\mathrm{tan}\:\frac{\pi}{\mathrm{15}}\:= \\ $$
Answered by 32 last updated on 29/Jul/17

$$ \\ $$
Answered by Tinkutara last updated on 29/Jul/17
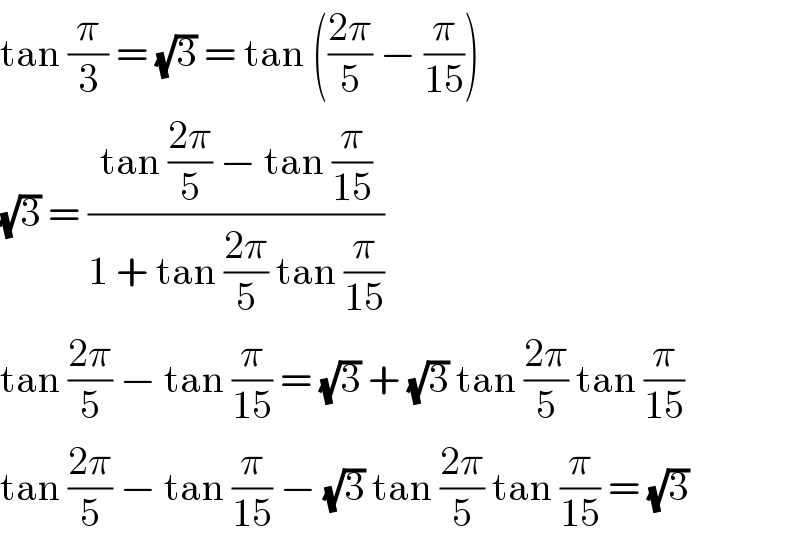
$$\mathrm{tan}\:\frac{\pi}{\mathrm{3}}\:=\:\sqrt{\mathrm{3}}\:=\:\mathrm{tan}\:\left(\frac{\mathrm{2}\pi}{\mathrm{5}}\:−\:\frac{\pi}{\mathrm{15}}\right) \\ $$$$\sqrt{\mathrm{3}}\:=\:\frac{\mathrm{tan}\:\frac{\mathrm{2}\pi}{\mathrm{5}}\:−\:\mathrm{tan}\:\frac{\pi}{\mathrm{15}}}{\mathrm{1}\:+\:\mathrm{tan}\:\frac{\mathrm{2}\pi}{\mathrm{5}}\:\mathrm{tan}\:\frac{\pi}{\mathrm{15}}} \\ $$$$\mathrm{tan}\:\frac{\mathrm{2}\pi}{\mathrm{5}}\:−\:\mathrm{tan}\:\frac{\pi}{\mathrm{15}}\:=\:\sqrt{\mathrm{3}}\:+\:\sqrt{\mathrm{3}}\:\mathrm{tan}\:\frac{\mathrm{2}\pi}{\mathrm{5}}\:\mathrm{tan}\:\frac{\pi}{\mathrm{15}} \\ $$$$\mathrm{tan}\:\frac{\mathrm{2}\pi}{\mathrm{5}}\:−\:\mathrm{tan}\:\frac{\pi}{\mathrm{15}}\:−\:\sqrt{\mathrm{3}}\:\mathrm{tan}\:\frac{\mathrm{2}\pi}{\mathrm{5}}\:\mathrm{tan}\:\frac{\pi}{\mathrm{15}}\:=\:\sqrt{\mathrm{3}} \\ $$
Answered by 32 last updated on 29/Jul/17

$$ \\ $$
