Question Number 54219 by 951172235v last updated on 31/Jan/19
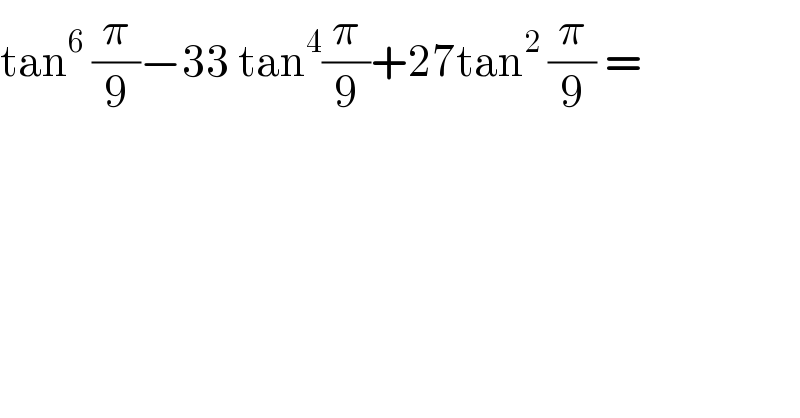
$$\mathrm{tan}^{\mathrm{6}} \:\frac{\pi}{\mathrm{9}}−\mathrm{33}\:\mathrm{tan}^{\mathrm{4}} \frac{\pi}{\mathrm{9}}+\mathrm{27tan}^{\mathrm{2}} \:\frac{\pi}{\mathrm{9}}\:=\: \\ $$
Answered by math1967 last updated on 31/Jan/19
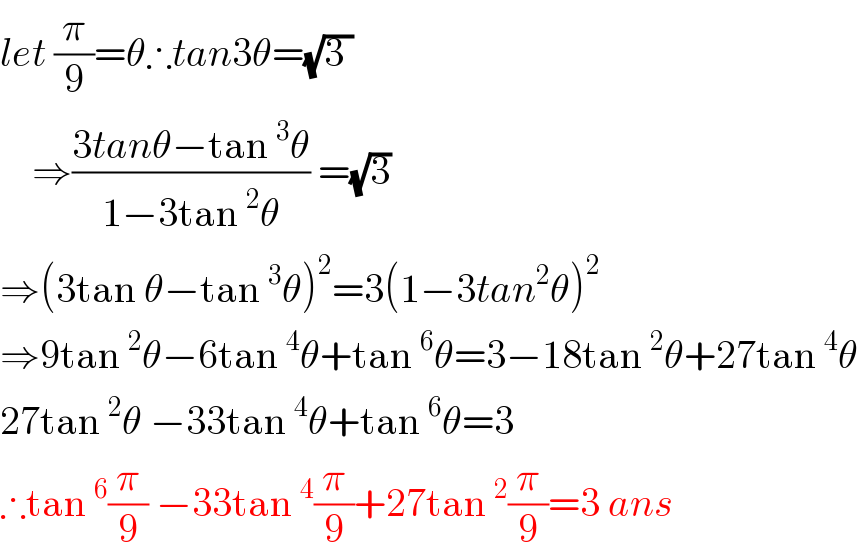
$${let}\:\frac{\pi}{\mathrm{9}}=\theta\therefore{tan}\mathrm{3}\theta=\sqrt{\mathrm{3}\:} \\ $$$$\:\:\:\:\Rightarrow\frac{\mathrm{3}{tan}\theta−\mathrm{tan}\:^{\mathrm{3}} \theta}{\mathrm{1}−\mathrm{3tan}\:^{\mathrm{2}} \theta}\:=\sqrt{\mathrm{3}}\: \\ $$$$\Rightarrow\left(\mathrm{3tan}\:\theta−\mathrm{tan}\:^{\mathrm{3}} \theta\right)^{\mathrm{2}} =\mathrm{3}\left(\mathrm{1}−\mathrm{3}{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{9tan}\:^{\mathrm{2}} \theta−\mathrm{6tan}\:^{\mathrm{4}} \theta+\mathrm{tan}\:^{\mathrm{6}} \theta=\mathrm{3}−\mathrm{18tan}\:^{\mathrm{2}} \theta+\mathrm{27tan}\:^{\mathrm{4}} \theta \\ $$$$\mathrm{27tan}\:^{\mathrm{2}} \theta\:−\mathrm{33tan}\:^{\mathrm{4}} \theta+\mathrm{tan}\:^{\mathrm{6}} \theta=\mathrm{3} \\ $$$$\therefore\mathrm{tan}\:^{\mathrm{6}} \frac{\pi}{\mathrm{9}}\:−\mathrm{33tan}\:^{\mathrm{4}} \frac{\pi}{\mathrm{9}}+\mathrm{27tan}\:^{\mathrm{2}} \frac{\pi}{\mathrm{9}}=\mathrm{3}\:{ans} \\ $$
