The-coefficient-of-the-middle-term-in-the-expansion-of-1-x-2n-is-

Question Number 18759 by 786786AM last updated on 29/Jul/17

The coefficient of the middle term in the

expansion of {(1 + x)}^{2 n} is

Answered by anuragbhandari123@gmail.com last updated on 29/Jul/17

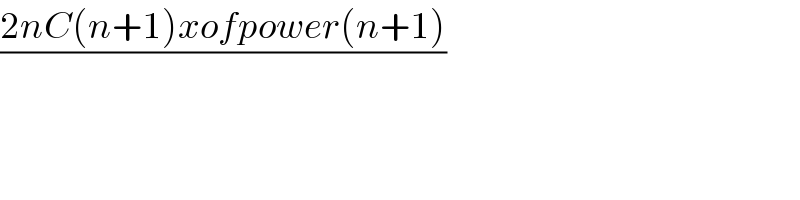
\frac{2 n C (n + 1) x o f p o w e r (n + 1)}{}

Answered by Tinkutara last updated on 30/Jul/17

Number of terms = 2 n + 1

Middle term = {(n + 1)}^{th} term

T_{n + 1} =^{2 n} C_{n} x^{n}

Coefficient of middle term =^{2 n} C_{n}

= \frac{(2 n)!}{n! n!} = \frac{1.2.3.4 \dots . (2 n - 2) (2 n - 1) (2 n)}{n! n!}

= \frac{[1.3.5 \dots . (2 n - 1)] [2.4.6 \dots . (2 n)]}{n! n!}

= \frac{[1.3.5 \dots . (2 n - 1)] 2^{n} [1.2.3 \dots . (n)]}{n! n!}

= \frac{1.3.5 \dots . (2 n - 1)}{n!} 2^{n}