Menu Close

The-coefficient-of-the-term-independent-of-x-in-the-expansion-of-x-1-x-2-3-x-1-3-1-x-1-x-x-1-2-10-is-

Tinku Tara 0 Comments
Pin




Question Number 115399 by EvoneAkashi last updated on 25/Sep/20
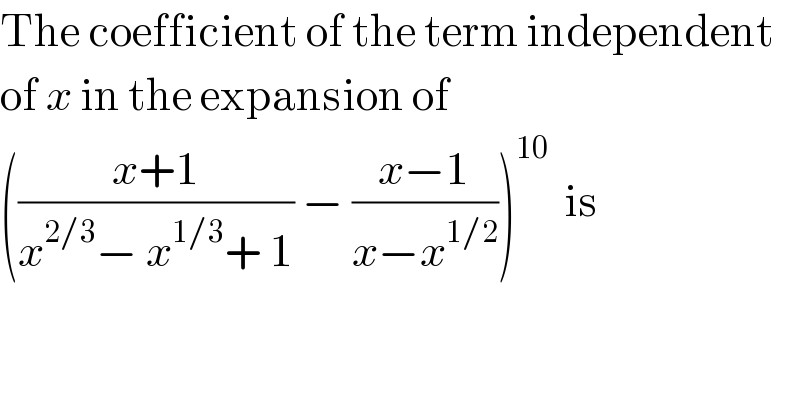
The coefficient of the term independent of x in the expansion of (((x+1)/(x^(2/3) − x^(1/3) + 1)) − ((x−1)/(x−x^(1/2) )))^(10) is
$$\mathrm{The}\:\mathrm{coefficient}\:\mathrm{of}\:\mathrm{the}\:\mathrm{term}\:\mathrm{independent} \\ $$$$\mathrm{of}\:{x}\:\mathrm{in}\:\mathrm{the}\:\mathrm{expansion}\:\mathrm{of} \\ $$$$\left(\frac{{x}+\mathrm{1}}{{x}^{\mathrm{2}/\mathrm{3}} −\:{x}^{\mathrm{1}/\mathrm{3}} +\:\mathrm{1}}\:−\:\frac{{x}−\mathrm{1}}{{x}−{x}^{\mathrm{1}/\mathrm{2}} }\right)^{\mathrm{10}} \:\:\mathrm{is} \\ $$
Answered by Dwaipayan Shikari last updated on 25/Sep/20
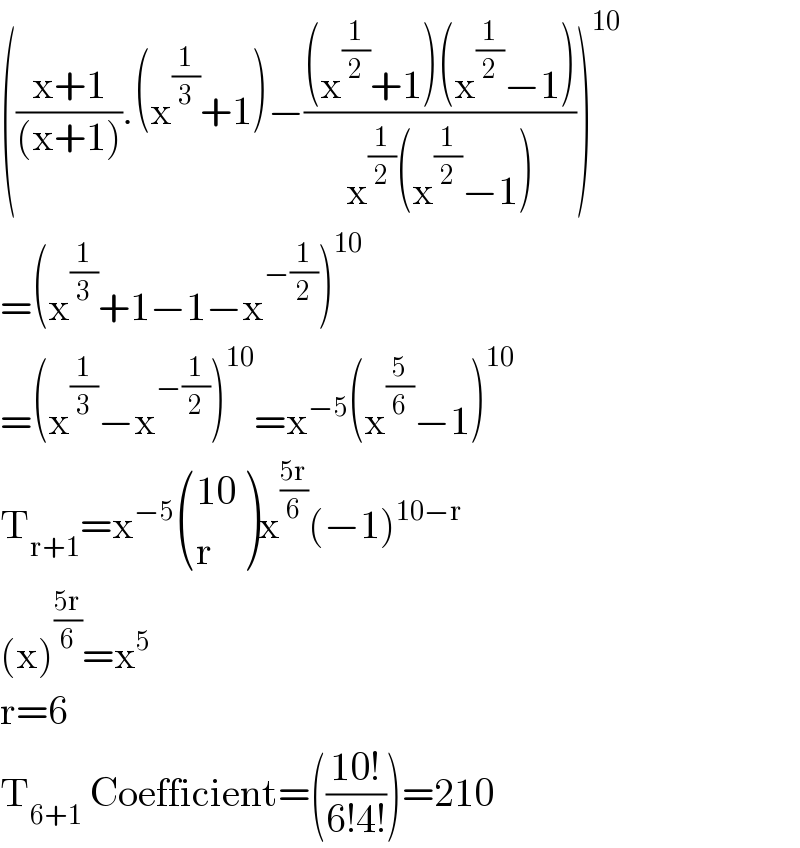
(((x+1)/((x+1))).(x^(1/3) +1)−(((x^(1/2) +1)(x^(1/2) −1))/(x^(1/2) (x^(1/2) −1))))^(10) =(x^(1/3) +1−1−x^(−(1/2)) )^(10) =(x^(1/3) −x^(−(1/2)) )^(10) =x^(−5) (x^(5/6) −1)^(10) T_(r+1) =x^(−5) (((10)),(r) )x^((5r)/6) (−1)^(10−r) (x)^((5r)/6) =x^5 r=6 T_(6+1) Coefficient=(((10!)/(6!4!)))=210
$$\left(\frac{\mathrm{x}+\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)}.\left(\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{3}}} +\mathrm{1}\right)−\frac{\left(\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{2}}} +\mathrm{1}\right)\left(\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{2}}} −\mathrm{1}\right)}{\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{2}}} −\mathrm{1}\right)}\right)^{\mathrm{10}} \\ $$$$=\left(\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{3}}} +\mathrm{1}−\mathrm{1}−\mathrm{x}^{−\frac{\mathrm{1}}{\mathrm{2}}} \right)^{\mathrm{10}} \\ $$$$=\left(\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{3}}} −\mathrm{x}^{−\frac{\mathrm{1}}{\mathrm{2}}} \right)^{\mathrm{10}} =\mathrm{x}^{−\mathrm{5}} \left(\mathrm{x}^{\frac{\mathrm{5}}{\mathrm{6}}} −\mathrm{1}\right)^{\mathrm{10}} \\ $$$$\mathrm{T}_{\mathrm{r}+\mathrm{1}} =\mathrm{x}^{−\mathrm{5}} \begin{pmatrix}{\mathrm{10}}\\{\mathrm{r}}\end{pmatrix}\mathrm{x}^{\frac{\mathrm{5r}}{\mathrm{6}}} \left(−\mathrm{1}\right)^{\mathrm{10}−\mathrm{r}} \\ $$$$\left(\mathrm{x}\right)^{\frac{\mathrm{5r}}{\mathrm{6}}} =\mathrm{x}^{\mathrm{5}} \\ $$$$\mathrm{r}=\mathrm{6} \\ $$$$\mathrm{T}_{\mathrm{6}+\mathrm{1}} \:\mathrm{Coefficient}=\left(\frac{\mathrm{10}!}{\mathrm{6}!\mathrm{4}!}\right)=\mathrm{210} \\ $$
Commented by mr W last updated on 25/Sep/20
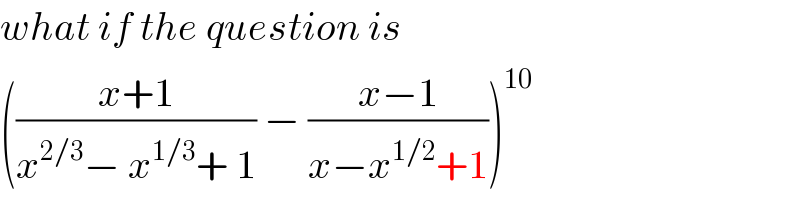
what if the question is (((x+1)/(x^(2/3) − x^(1/3) + 1)) − ((x−1)/(x−x^(1/2) +1)))^(10)
$${what}\:{if}\:{the}\:{question}\:{is} \\ $$$$\left(\frac{{x}+\mathrm{1}}{{x}^{\mathrm{2}/\mathrm{3}} −\:{x}^{\mathrm{1}/\mathrm{3}} +\:\mathrm{1}}\:−\:\frac{{x}−\mathrm{1}}{{x}−{x}^{\mathrm{1}/\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{10}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *