Menu Close

The-coefficient-of-x-4-in-the-expansion-of-x-2-3-x-2-10-is-

Tinku Tara 0 Comments
Pin




Question Number 42684 by 1996ajaykmar@email.com last updated on 31/Aug/18
The coefficient of x^4 in the expansion of ((x/2) − (3/x^2 ))^(10) is
$$\mathrm{The}\:\mathrm{coefficient}\:\mathrm{of}\:{x}^{\mathrm{4}} \:\mathrm{in}\:\mathrm{the}\:\mathrm{expansion}\:\mathrm{of} \\ $$$$\left(\frac{{x}}{\mathrm{2}}\:−\:\frac{\mathrm{3}}{{x}^{\mathrm{2}} }\right)^{\mathrm{10}} \:\mathrm{is} \\ $$
Commented by maxmathsup by imad last updated on 31/Aug/18
let p(x) = ((x/2) −(3/x^2 ))^(10) ⇒p(x)=(1/(2^(10) x^(20) ))(x^3 −6)^(10) = 2^(−10) x^(−20) Σ_(k=0) ^(10) C_(10) ^k x^(3k) (−6)^(10−k) =2^(−10) Σ_(k=0) ^(10) C_(10) ^k x^(3k−20) (−6)^(10−3k) the coefficient x^4 is obtained when 3k−20 =4 ⇒k =8 ⇒ λ_4 = 2^(−10) C_(10) ^8 (−6)^(10−24) =2^(−10) (−6)^(−14) C_(10) ^8 = (2^(−10) /6^(14) ) C_(10) ^8 = (2^(−10) /(2^(14) .3^(14) )) ((10!)/(8!2!)) = (1/(2^(24) .3^(14) )) (45) = ((45)/(2^(24) 3^(13) )) = ((3^2 .5)/(2^(24) 3^(13) )) =(5/(2^(24) .3^(11) )) .
$${let}\:{p}\left({x}\right)\:=\:\left(\frac{{x}}{\mathrm{2}}\:−\frac{\mathrm{3}}{{x}^{\mathrm{2}} }\right)^{\mathrm{10}} \:\Rightarrow{p}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{10}} \:{x}^{\mathrm{20}} }\left({x}^{\mathrm{3}} −\mathrm{6}\right)^{\mathrm{10}} \\ $$$$=\:\mathrm{2}^{−\mathrm{10}} \:{x}^{−\mathrm{20}} \:\sum_{{k}=\mathrm{0}} ^{\mathrm{10}} \:{C}_{\mathrm{10}} ^{{k}} \:\:{x}^{\mathrm{3}{k}} \:\left(−\mathrm{6}\right)^{\mathrm{10}−{k}} \:=\mathrm{2}^{−\mathrm{10}} \:\sum_{{k}=\mathrm{0}} ^{\mathrm{10}} \:\:{C}_{\mathrm{10}} ^{{k}} \:{x}^{\mathrm{3}{k}−\mathrm{20}} \:\left(−\mathrm{6}\right)^{\mathrm{10}−\mathrm{3}{k}} \:\:\: \\ $$$${the}\:{coefficient}\:{x}^{\mathrm{4}} \:{is}\:{obtained}\:{when}\:\mathrm{3}{k}−\mathrm{20}\:=\mathrm{4}\:\Rightarrow{k}\:=\mathrm{8}\:\Rightarrow \\ $$$$\lambda_{\mathrm{4}} =\:\mathrm{2}^{−\mathrm{10}} \:\:{C}_{\mathrm{10}} ^{\mathrm{8}} \:\:\left(−\mathrm{6}\right)^{\mathrm{10}−\mathrm{24}} \:=\mathrm{2}^{−\mathrm{10}} \:\:\left(−\mathrm{6}\right)^{−\mathrm{14}} \:\:\:{C}_{\mathrm{10}} ^{\mathrm{8}} \:\:\:=\:\frac{\mathrm{2}^{−\mathrm{10}} }{\mathrm{6}^{\mathrm{14}} }\:\:{C}_{\mathrm{10}} ^{\mathrm{8}} \\ $$$$=\:\frac{\mathrm{2}^{−\mathrm{10}} }{\mathrm{2}^{\mathrm{14}} \:.\mathrm{3}^{\mathrm{14}} }\:\frac{\mathrm{10}!}{\mathrm{8}!\mathrm{2}!}\:=\:\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{24}} \:.\mathrm{3}^{\mathrm{14}} }\:\left(\mathrm{45}\right)\:=\:\frac{\mathrm{45}}{\mathrm{2}^{\mathrm{24}} \:\mathrm{3}^{\mathrm{13}} }\:=\:\frac{\mathrm{3}^{\mathrm{2}} \:.\mathrm{5}}{\mathrm{2}^{\mathrm{24}} \:\mathrm{3}^{\mathrm{13}} }\:=\frac{\mathrm{5}}{\mathrm{2}^{\mathrm{24}} \:.\mathrm{3}^{\mathrm{11}} }\:\:. \\ $$
Commented by Rio Michael last updated on 31/Aug/18
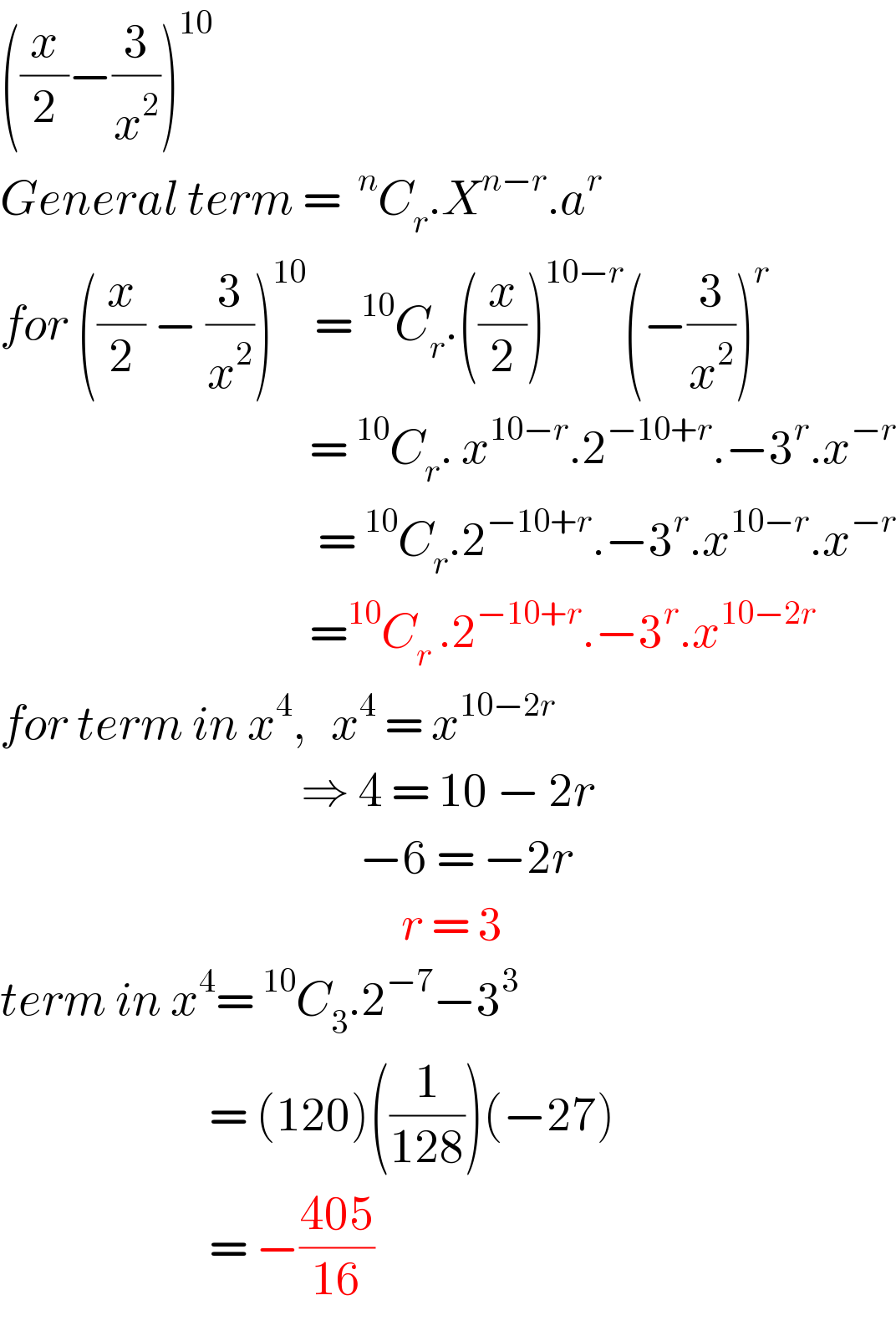
((x/2)−(3/x^2 ))^(10) General term = ^n C_r .X^(n−r) .a^(r ) for ((x/2) − (3/x^2 ))^(10) =^(10) C_r .((x/2))^(10−r) (−(3/x^2 ))^r =^(10) C_r . x^(10−r) .2^(−10+r) .−3^r .x^(−r) =^(10) C_r .2^(−10+r) .−3^r .x^(10−r) .x^(−r) =^(10) C_(r ) .2^(−10+r) .−3^r .x^(10−2r) for term in x^4 , x^4 = x^(10−2r) ⇒ 4 = 10 − 2r −6 = −2r r = 3 term in x^4 =^(10) C_3 .2^(−7) −3^3 = (120)((1/(128)))(−27) = −((405)/(16))
$$\left(\frac{{x}}{\mathrm{2}}−\frac{\mathrm{3}}{{x}^{\mathrm{2}} }\right)^{\mathrm{10}} \\ $$$${General}\:{term}\:=\:\:^{{n}} {C}_{{r}} .{X}^{{n}−{r}} .{a}^{{r}\:} \\ $$$${for}\:\left(\frac{{x}}{\mathrm{2}}\:−\:\frac{\mathrm{3}}{{x}^{\mathrm{2}} }\right)^{\mathrm{10}} \:=\:^{\mathrm{10}} {C}_{{r}} .\left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{10}−{r}} \left(−\frac{\mathrm{3}}{{x}^{\mathrm{2}} }\right)^{{r}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:^{\mathrm{10}} {C}_{{r}} .\:{x}^{\mathrm{10}−{r}} .\mathrm{2}^{−\mathrm{10}+{r}} .−\mathrm{3}^{{r}} .{x}^{−{r}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:^{\mathrm{10}} {C}_{{r}} .\mathrm{2}^{−\mathrm{10}+{r}} .−\mathrm{3}^{{r}} .{x}^{\mathrm{10}−{r}} .{x}^{−{r}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=^{\mathrm{10}} {C}_{{r}\:} .\mathrm{2}^{−\mathrm{10}+{r}} .−\mathrm{3}^{{r}} .{x}^{\mathrm{10}−\mathrm{2}{r}} \\ $$$${for}\:{term}\:{in}\:{x}^{\mathrm{4}} ,\:\:\:{x}^{\mathrm{4}} \:=\:{x}^{\mathrm{10}−\mathrm{2}{r}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\mathrm{4}\:=\:\mathrm{10}\:−\:\mathrm{2}{r} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{6}\:=\:−\mathrm{2}{r} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{r}\:=\:\mathrm{3} \\ $$$${term}\:{in}\:{x}^{\mathrm{4}} =\:^{\mathrm{10}} {C}_{\mathrm{3}} .\mathrm{2}^{−\mathrm{7}} −\mathrm{3}^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\left(\mathrm{120}\right)\left(\frac{\mathrm{1}}{\mathrm{128}}\right)\left(−\mathrm{27}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:−\frac{\mathrm{405}}{\mathrm{16}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *