Question Number 56095 by gunawan last updated on 10/Mar/19
$$\mathrm{The}\:\mathrm{coefficient}\:\mathrm{of}\:{x}^{\mathrm{5}} \:\mathrm{in}\:\mathrm{the}\:\mathrm{expansion}\:\mathrm{of} \\ $$$$\left(\mathrm{1}+{x}\right)^{\mathrm{21}} \:+\left(\mathrm{1}+{x}\right)^{\mathrm{22}} +…+\left(\mathrm{1}+{x}\right)^{\mathrm{30}} \:\:\mathrm{is} \\ $$
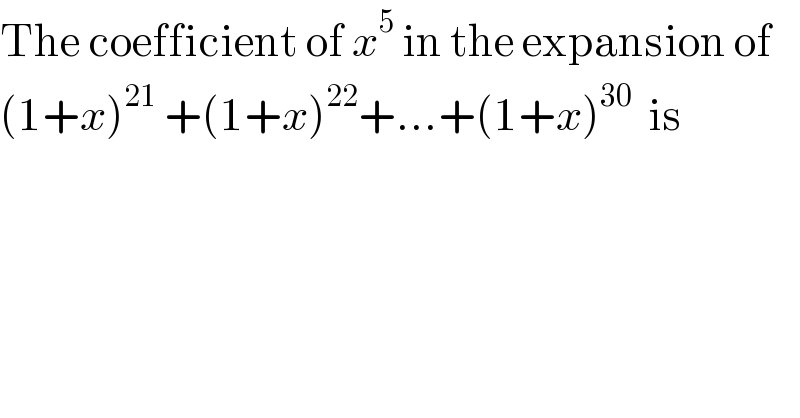
Answered by tanmay.chaudhury50@gmail.com last updated on 10/Mar/19
$$\left(\mathrm{1}+{x}\right)^{{n}} \\ $$$${let}\:\left({r}+\mathrm{1}\right){th}\:{term}\:{contains}\:{x}^{\mathrm{5}} \\ $$$${nc}_{{r}} {x}^{{r}} \rightarrow{so}\:{x}^{{r}} ={x}^{\mathrm{5}} \rightarrow{r}=\mathrm{5} \\ $$$${now}\:\left(\mathrm{1}+{x}\right)^{\mathrm{21}} \:\rightarrow\mathrm{21}{c}_{\mathrm{5}} {x}^{\mathrm{5}} \\ $$$$\left(\mathrm{1}+{x}\right)^{\mathrm{22}} \rightarrow\mathrm{22}{c}_{\mathrm{5}} {x}^{\mathrm{5}} \\ $$$$… \\ $$$$… \\ $$$${required}\:{answer}\:{is} \\ $$$$\mathrm{21}{c}_{\mathrm{5}} +\mathrm{22}{c}_{\mathrm{5}} +\mathrm{23}{c}_{\mathrm{5}} +…+\mathrm{30}{c}_{\mathrm{5}} \\ $$
Answered by mr W last updated on 10/Mar/19
![(1+x)^(21) +(1+x)^(22) +...+(1+x)^(30) =(((1+x)^(21) [(1+x)^(10) −1])/((1+x)−1)) =(((1+x)^(31) −(1+x)^(21) )/x) coef. of x^5 term is: C_6 ^(31) −C_6 ^(21) =682017](https://www.tinkutara.com/question/Q56106.png)
$$\left(\mathrm{1}+{x}\right)^{\mathrm{21}} \:+\left(\mathrm{1}+{x}\right)^{\mathrm{22}} +…+\left(\mathrm{1}+{x}\right)^{\mathrm{30}} \\ $$$$=\frac{\left(\mathrm{1}+{x}\right)^{\mathrm{21}} \left[\left(\mathrm{1}+{x}\right)^{\mathrm{10}} −\mathrm{1}\right]}{\left(\mathrm{1}+{x}\right)−\mathrm{1}} \\ $$$$=\frac{\left(\mathrm{1}+{x}\right)^{\mathrm{31}} −\left(\mathrm{1}+{x}\right)^{\mathrm{21}} }{{x}} \\ $$$${coef}.\:{of}\:{x}^{\mathrm{5}} \:{term}\:{is}: \\ $$$${C}_{\mathrm{6}} ^{\mathrm{31}} −{C}_{\mathrm{6}} ^{\mathrm{21}} =\mathrm{682017} \\ $$
Commented by gunawan last updated on 10/Mar/19
$$\mathrm{wow}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{Sir} \\ $$
Commented by malwaan last updated on 10/Mar/19
$$\boldsymbol{{what}}\:\boldsymbol{{is}}\:\boldsymbol{{the}}\:\boldsymbol{{formula}}\: \\ $$$$\boldsymbol{{that}}\:\boldsymbol{{you}}\:\boldsymbol{{used}}\:?\:\boldsymbol{{please}} \\ $$
Commented by mr W last updated on 10/Mar/19
![S=(1+x)^(21) +(1+x)^(22) +...+(1+x)^(30) is a geometric progression with a_1 =(1+x)^(21) q=(1+x) n=10 S=((a_1 (q^n −1))/(q−1))=(((1+x)^(21) [(1+x)^(10) −1])/((1+x)−1)) =(((1+x)^(31) −(1+x)^(21) )/x) x^6 term of (1+x)^(31) is C_6 ^(31) x^6 x^6 term of (1+x)^(21) is C_6 ^(21) x^6 x^5 term of S is ((C_6 ^(31) x^6 −C_6 ^(21) x^6 )/x)=(C_6 ^(31) −C_6 ^(21) )x^5](https://www.tinkutara.com/question/Q56128.png)
$${S}=\left(\mathrm{1}+{x}\right)^{\mathrm{21}} \:+\left(\mathrm{1}+{x}\right)^{\mathrm{22}} +…+\left(\mathrm{1}+{x}\right)^{\mathrm{30}} \\ $$$${is}\:{a}\:{geometric}\:{progression}\:{with} \\ $$$${a}_{\mathrm{1}} =\left(\mathrm{1}+{x}\right)^{\mathrm{21}} \\ $$$${q}=\left(\mathrm{1}+{x}\right) \\ $$$${n}=\mathrm{10} \\ $$$${S}=\frac{{a}_{\mathrm{1}} \left({q}^{{n}} −\mathrm{1}\right)}{{q}−\mathrm{1}}=\frac{\left(\mathrm{1}+{x}\right)^{\mathrm{21}} \left[\left(\mathrm{1}+{x}\right)^{\mathrm{10}} −\mathrm{1}\right]}{\left(\mathrm{1}+{x}\right)−\mathrm{1}} \\ $$$$=\frac{\left(\mathrm{1}+{x}\right)^{\mathrm{31}} −\left(\mathrm{1}+{x}\right)^{\mathrm{21}} }{{x}} \\ $$$${x}^{\mathrm{6}} \:{term}\:{of}\:\left(\mathrm{1}+{x}\right)^{\mathrm{31}} \:{is}\:{C}_{\mathrm{6}} ^{\mathrm{31}} {x}^{\mathrm{6}} \\ $$$${x}^{\mathrm{6}} \:{term}\:{of}\:\left(\mathrm{1}+{x}\right)^{\mathrm{21}} \:{is}\:{C}_{\mathrm{6}} ^{\mathrm{21}} {x}^{\mathrm{6}} \\ $$$${x}^{\mathrm{5}} \:{term}\:{of}\:{S}\:{is}\:\frac{{C}_{\mathrm{6}} ^{\mathrm{31}} {x}^{\mathrm{6}} −{C}_{\mathrm{6}} ^{\mathrm{21}} {x}^{\mathrm{6}} }{{x}}=\left({C}_{\mathrm{6}} ^{\mathrm{31}} −{C}_{\mathrm{6}} ^{\mathrm{21}} \right){x}^{\mathrm{5}} \\ $$
Commented by malwaan last updated on 11/Mar/19
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$