Question Number 62086 by Cypher1207 last updated on 15/Jun/19
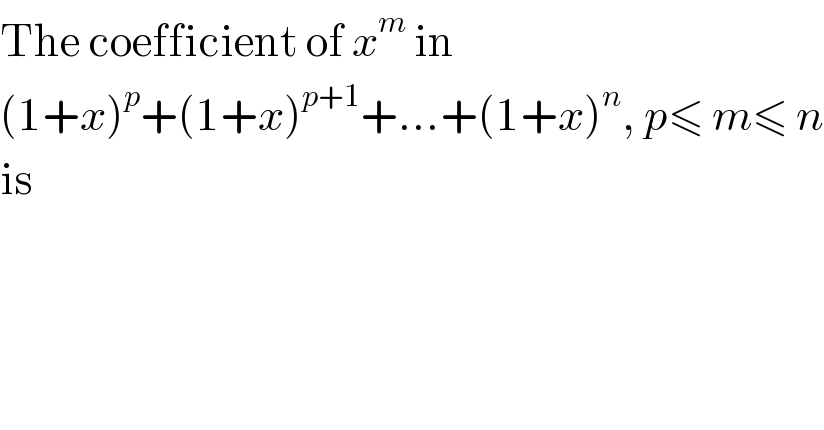
$$\mathrm{The}\:\mathrm{coefficient}\:\mathrm{of}\:{x}^{{m}} \:\mathrm{in} \\ $$$$\left(\mathrm{1}+{x}\right)^{{p}} +\left(\mathrm{1}+{x}\right)^{{p}+\mathrm{1}} +…+\left(\mathrm{1}+{x}\right)^{{n}} ,\:{p}\leqslant\:{m}\leqslant\:{n} \\ $$$$\mathrm{is}\: \\ $$
Answered by mr W last updated on 15/Jun/19
![(1+x)^p +(1+x)^(p+1) +...+(1+x)^n ← GP =(((1+x)^p [(1+x)^(n−p+1) −1])/((1+x)−1)) =(((1+x)^(n+1) −(1+x)^p )/x) =(1/x)[Σ_(k=0) ^(n+1) C_k ^(n+1) x^k −Σ_(k=0) ^p C_k ^p x^k ] =(1/x)[Σ_(k=0) ^p C_k ^(n+1) x^k −Σ_(k=0) ^p C_k ^p x^k +Σ_(k=p+1) ^(n+1) C_k ^(n+1) x^k ] =(1/x)[Σ_(k=0) ^p (C_k ^(n+1) −C_k ^p )x^k +Σ_(k=p+1) ^(n+1) C_k ^(n+1) x^k ] =Σ_(k=0) ^p (C_k ^(n+1) −C_k ^p )x^(k−1) +Σ_(k=p+1) ^(n+1) C_k ^(n+1) x^(k−1) =Σ_(k=0) ^(p−1) (C_(k+1) ^(n+1) −C_(k+1) ^p )x^k +Σ_(k=p) ^n C_(k+1) ^(n+1) x^k =Σ_(k=0) ^n a_k x^k with a_k = { ((C_(k+1) ^(n+1) −C_(k+1) ^p for 0≤k≤p−1)),((C_(k+1) ^(n+1) for p≤k≤n)) :} for p≤m≤n, coef. of x^m is C_(m+1) ^(n+1) .](https://www.tinkutara.com/question/Q62095.png)
$$\left(\mathrm{1}+{x}\right)^{{p}} +\left(\mathrm{1}+{x}\right)^{{p}+\mathrm{1}} +…+\left(\mathrm{1}+{x}\right)^{{n}} \:\:\:\:\leftarrow\:{GP} \\ $$$$=\frac{\left(\mathrm{1}+{x}\right)^{{p}} \left[\left(\mathrm{1}+{x}\right)^{{n}−{p}+\mathrm{1}} −\mathrm{1}\right]}{\left(\mathrm{1}+{x}\right)−\mathrm{1}} \\ $$$$=\frac{\left(\mathrm{1}+{x}\right)^{{n}+\mathrm{1}} −\left(\mathrm{1}+{x}\right)^{{p}} }{{x}} \\ $$$$=\frac{\mathrm{1}}{{x}}\left[\underset{{k}=\mathrm{0}} {\overset{{n}+\mathrm{1}} {\sum}}{C}_{{k}} ^{{n}+\mathrm{1}} {x}^{{k}} −\underset{{k}=\mathrm{0}} {\overset{{p}} {\sum}}{C}_{{k}} ^{{p}} {x}^{{k}} \right] \\ $$$$=\frac{\mathrm{1}}{{x}}\left[\underset{{k}=\mathrm{0}} {\overset{{p}} {\sum}}{C}_{{k}} ^{{n}+\mathrm{1}} {x}^{{k}} −\underset{{k}=\mathrm{0}} {\overset{{p}} {\sum}}{C}_{{k}} ^{{p}} {x}^{{k}} +\underset{{k}={p}+\mathrm{1}} {\overset{{n}+\mathrm{1}} {\sum}}{C}_{{k}} ^{{n}+\mathrm{1}} {x}^{{k}} \right] \\ $$$$=\frac{\mathrm{1}}{{x}}\left[\underset{{k}=\mathrm{0}} {\overset{{p}} {\sum}}\left({C}_{{k}} ^{{n}+\mathrm{1}} −{C}_{{k}} ^{{p}} \right){x}^{{k}} +\underset{{k}={p}+\mathrm{1}} {\overset{{n}+\mathrm{1}} {\sum}}{C}_{{k}} ^{{n}+\mathrm{1}} {x}^{{k}} \right] \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{p}} {\sum}}\left({C}_{{k}} ^{{n}+\mathrm{1}} −{C}_{{k}} ^{{p}} \right){x}^{{k}−\mathrm{1}} +\underset{{k}={p}+\mathrm{1}} {\overset{{n}+\mathrm{1}} {\sum}}{C}_{{k}} ^{{n}+\mathrm{1}} {x}^{{k}−\mathrm{1}} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{p}−\mathrm{1}} {\sum}}\left({C}_{{k}+\mathrm{1}} ^{{n}+\mathrm{1}} −{C}_{{k}+\mathrm{1}} ^{{p}} \right){x}^{{k}} +\underset{{k}={p}} {\overset{{n}} {\sum}}{C}_{{k}+\mathrm{1}} ^{{n}+\mathrm{1}} {x}^{{k}} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{{k}} {x}^{{k}} \\ $$$${with}\:{a}_{{k}} =\begin{cases}{{C}_{{k}+\mathrm{1}} ^{{n}+\mathrm{1}} −{C}_{{k}+\mathrm{1}} ^{{p}} \:{for}\:\mathrm{0}\leqslant{k}\leqslant{p}−\mathrm{1}}\\{{C}_{{k}+\mathrm{1}} ^{{n}+\mathrm{1}} \:{for}\:{p}\leqslant{k}\leqslant{n}}\end{cases} \\ $$$${for}\:{p}\leqslant{m}\leqslant{n}, \\ $$$${coef}.\:{of}\:{x}^{{m}} \:{is}\:{C}_{{m}+\mathrm{1}} ^{{n}+\mathrm{1}} . \\ $$
