Question Number 21174 by akinyeni last updated on 15/Sep/17
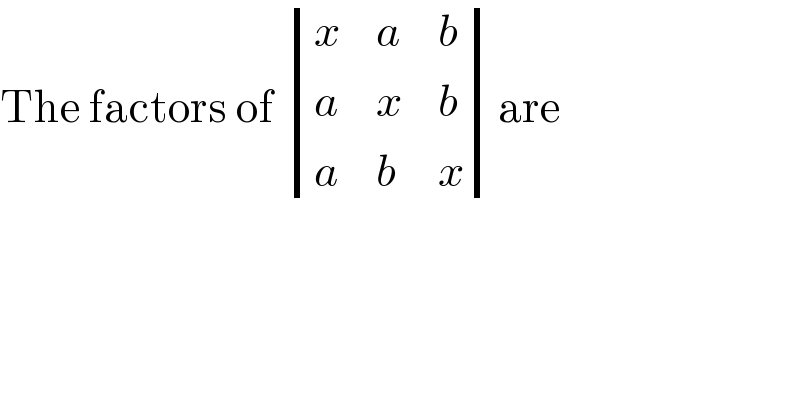
$$\mathrm{The}\:\mathrm{factors}\:\mathrm{of}\:\begin{vmatrix}{{x}}&{{a}}&{{b}}\\{{a}}&{{x}}&{{b}}\\{{a}}&{{b}}&{{x}}\end{vmatrix}\mathrm{are} \\ $$
Answered by $@ty@m last updated on 15/Sep/17
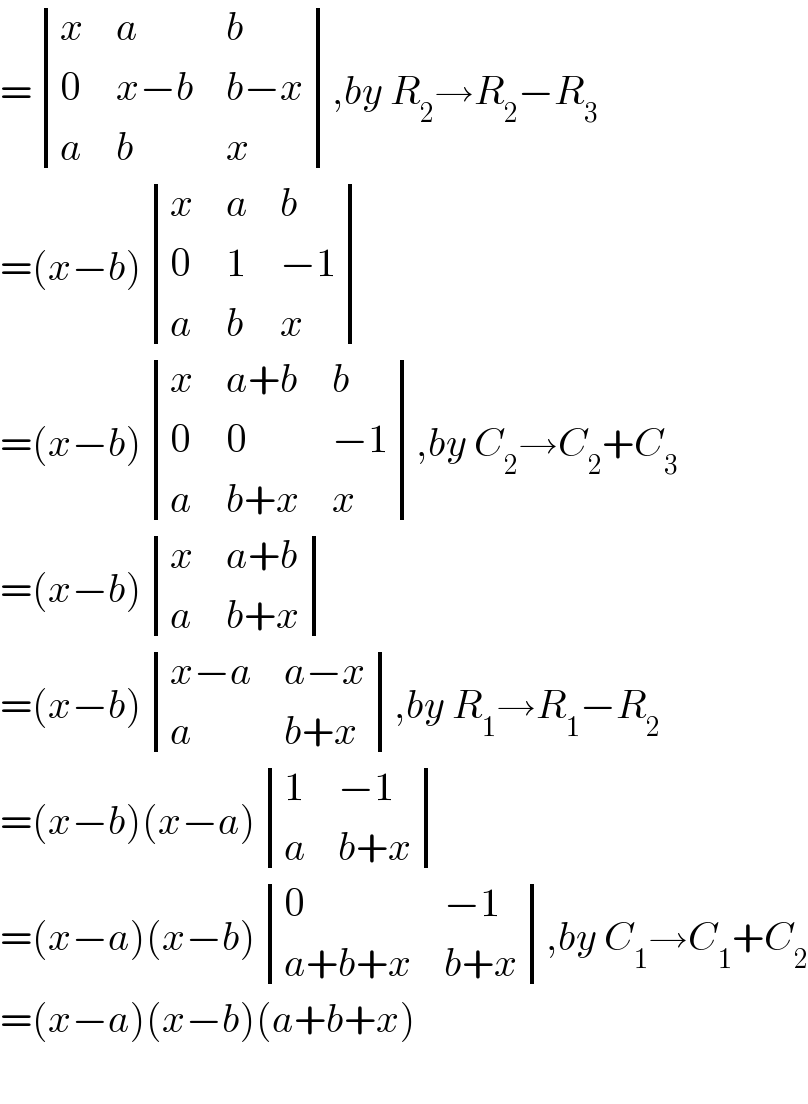
$$=\begin{vmatrix}{{x}}&{{a}}&{{b}}\\{\mathrm{0}}&{{x}−{b}}&{{b}−{x}}\\{{a}}&{{b}}&{{x}}\end{vmatrix},{by}\:{R}_{\mathrm{2}} \rightarrow{R}_{\mathrm{2}} −{R}_{\mathrm{3}} \\ $$$$=\left({x}−{b}\right)\begin{vmatrix}{{x}}&{{a}}&{{b}}\\{\mathrm{0}}&{\mathrm{1}}&{−\mathrm{1}}\\{{a}}&{{b}}&{{x}}\end{vmatrix} \\ $$$$=\left({x}−{b}\right)\begin{vmatrix}{{x}}&{{a}+{b}}&{{b}}\\{\mathrm{0}}&{\mathrm{0}}&{−\mathrm{1}}\\{{a}}&{{b}+{x}}&{{x}}\end{vmatrix},{by}\:{C}_{\mathrm{2}} \rightarrow{C}_{\mathrm{2}} +{C}_{\mathrm{3}} \\ $$$$=\left({x}−{b}\right)\begin{vmatrix}{{x}}&{{a}+{b}}\\{{a}}&{{b}+{x}}\end{vmatrix} \\ $$$$=\left({x}−{b}\right)\begin{vmatrix}{{x}−{a}}&{{a}−{x}}\\{{a}}&{{b}+{x}}\end{vmatrix},{by}\:{R}_{\mathrm{1}} \rightarrow{R}_{\mathrm{1}} −{R}_{\mathrm{2}} \\ $$$$=\left({x}−{b}\right)\left({x}−{a}\right)\begin{vmatrix}{\mathrm{1}}&{−\mathrm{1}}\\{{a}}&{{b}+{x}}\end{vmatrix} \\ $$$$=\left({x}−{a}\right)\left({x}−{b}\right)\begin{vmatrix}{\mathrm{0}}&{−\mathrm{1}}\\{{a}+{b}+{x}}&{{b}+{x}}\end{vmatrix},{by}\:{C}_{\mathrm{1}} \rightarrow{C}_{\mathrm{1}} +{C}_{\mathrm{2}} \\ $$$$=\left({x}−{a}\right)\left({x}−{b}\right)\left({a}+{b}+{x}\right) \\ $$$$ \\ $$
