Question Number 8107 by Nadium last updated on 30/Sep/16

$$\mathrm{The}\:\mathrm{general}\:\mathrm{term}\:\mathrm{in}\:\mathrm{the}\:\mathrm{expansion}\:\mathrm{of} \\ $$$$\left(\mathrm{1}−\mathrm{2}{x}\right)^{\mathrm{3}/\mathrm{4}} \:\:\mathrm{is} \\ $$
Answered by prakash jain last updated on 30/Sep/16
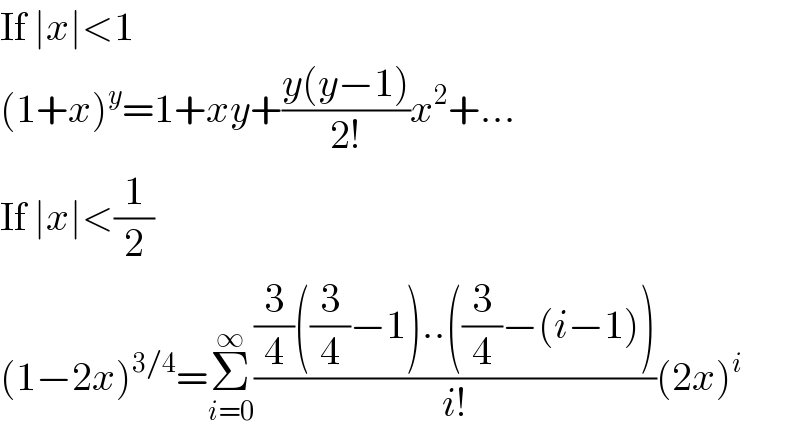
$$\mathrm{If}\:\mid{x}\mid<\mathrm{1} \\ $$$$\left(\mathrm{1}+{x}\right)^{{y}} =\mathrm{1}+{xy}+\frac{{y}\left({y}−\mathrm{1}\right)}{\mathrm{2}!}{x}^{\mathrm{2}} +… \\ $$$$\mathrm{If}\:\mid{x}\mid<\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left(\mathrm{1}−\mathrm{2}{x}\right)^{\mathrm{3}/\mathrm{4}} =\underset{{i}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\frac{\mathrm{3}}{\mathrm{4}}\left(\frac{\mathrm{3}}{\mathrm{4}}−\mathrm{1}\right)..\left(\frac{\mathrm{3}}{\mathrm{4}}−\left({i}−\mathrm{1}\right)\right)}{{i}!}\left(\mathrm{2}{x}\right)^{{i}} \\ $$
