Question Number 43642 by gunawan last updated on 13/Sep/18
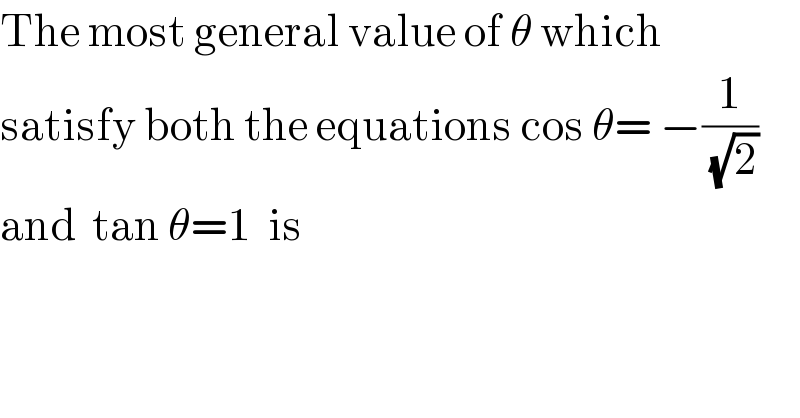
$$\mathrm{The}\:\mathrm{most}\:\mathrm{general}\:\mathrm{value}\:\mathrm{of}\:\theta\:\mathrm{which} \\ $$$$\mathrm{satisfy}\:\mathrm{both}\:\mathrm{the}\:\mathrm{equations}\:\mathrm{cos}\:\theta=\:−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\mathrm{and}\:\:\mathrm{tan}\:\theta=\mathrm{1}\:\:\mathrm{is} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 13/Sep/18
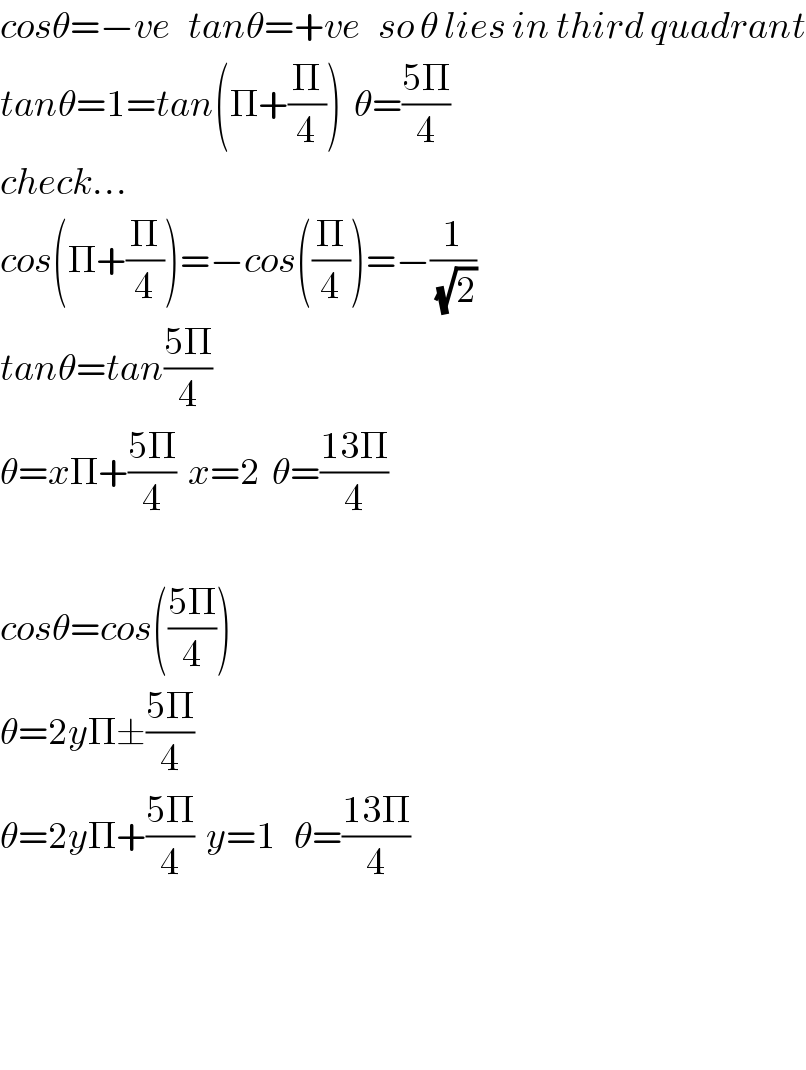
$${cos}\theta=−{ve}\:\:\:{tan}\theta=+{ve}\:\:\:{so}\:\theta\:{lies}\:{in}\:{third}\:{quadrant} \\ $$$${tan}\theta=\mathrm{1}={tan}\left(\Pi+\frac{\Pi}{\mathrm{4}}\right)\:\:\theta=\frac{\mathrm{5}\Pi}{\mathrm{4}} \\ $$$${check}… \\ $$$${cos}\left(\Pi+\frac{\Pi}{\mathrm{4}}\right)=−{cos}\left(\frac{\Pi}{\mathrm{4}}\right)=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$${tan}\theta={tan}\frac{\mathrm{5}\Pi}{\mathrm{4}} \\ $$$$\theta={x}\Pi+\frac{\mathrm{5}\Pi}{\mathrm{4}}\:\:{x}=\mathrm{2}\:\:\theta=\frac{\mathrm{13}\Pi}{\mathrm{4}} \\ $$$$ \\ $$$${cos}\theta={cos}\left(\frac{\mathrm{5}\Pi}{\mathrm{4}}\right) \\ $$$$\theta=\mathrm{2}{y}\Pi\pm\frac{\mathrm{5}\Pi}{\mathrm{4}} \\ $$$$\theta=\mathrm{2}{y}\Pi+\frac{\mathrm{5}\Pi}{\mathrm{4}}\:\:{y}=\mathrm{1}\:\:\:\theta=\frac{\mathrm{13}\Pi}{\mathrm{4}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
