Menu Close

The-nth-term-of-the-series-4-14-30-52-80-114-is-

Tinku Tara 0 Comments
Pin




Question Number 56417 by gunawan last updated on 16/Mar/19
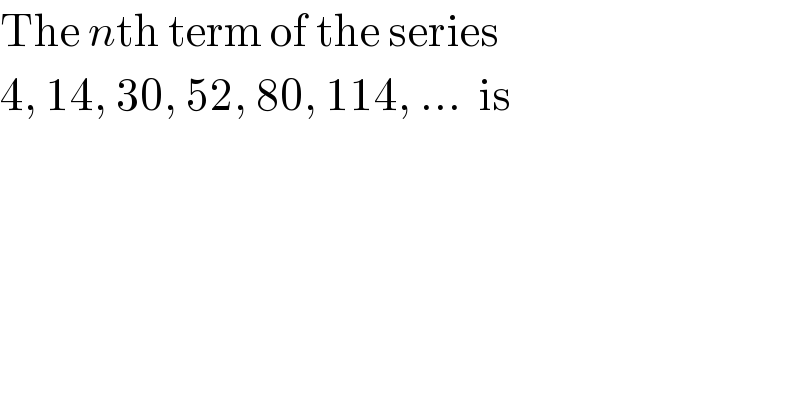
The nth term of the series 4, 14, 30, 52, 80, 114, ... is
$$\mathrm{The}\:{n}\mathrm{th}\:\mathrm{term}\:\mathrm{of}\:\mathrm{the}\:\mathrm{series}\: \\ $$$$\mathrm{4},\:\mathrm{14},\:\mathrm{30},\:\mathrm{52},\:\mathrm{80},\:\mathrm{114},\:…\:\:\mathrm{is} \\ $$
Answered by MJS last updated on 16/Mar/19
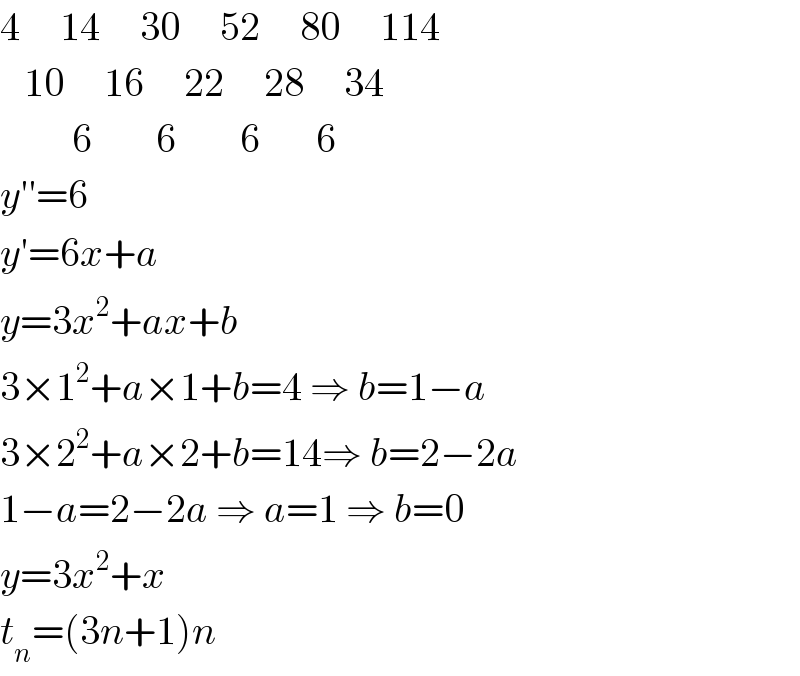
4 14 30 52 80 114 10 16 22 28 34 6 6 6 6 y′′=6 y′=6x+a y=3x^2 +ax+b 3×1^2 +a×1+b=4 ⇒ b=1−a 3×2^2 +a×2+b=14⇒ b=2−2a 1−a=2−2a ⇒ a=1 ⇒ b=0 y=3x^2 +x t_n =(3n+1)n
$$\mathrm{4}\:\:\:\:\:\mathrm{14}\:\:\:\:\:\mathrm{30}\:\:\:\:\:\mathrm{52}\:\:\:\:\:\mathrm{80}\:\:\:\:\:\mathrm{114} \\ $$$$\:\:\:\mathrm{10}\:\:\:\:\:\mathrm{16}\:\:\:\:\:\mathrm{22}\:\:\:\:\:\mathrm{28}\:\:\:\:\:\mathrm{34} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{6}\:\:\:\:\:\:\:\:\mathrm{6}\:\:\:\:\:\:\:\:\mathrm{6}\:\:\:\:\:\:\:\mathrm{6} \\ $$$${y}''=\mathrm{6} \\ $$$${y}'=\mathrm{6}{x}+{a} \\ $$$${y}=\mathrm{3}{x}^{\mathrm{2}} +{ax}+{b} \\ $$$$\mathrm{3}×\mathrm{1}^{\mathrm{2}} +{a}×\mathrm{1}+{b}=\mathrm{4}\:\Rightarrow\:{b}=\mathrm{1}−{a} \\ $$$$\mathrm{3}×\mathrm{2}^{\mathrm{2}} +{a}×\mathrm{2}+{b}=\mathrm{14}\Rightarrow\:{b}=\mathrm{2}−\mathrm{2}{a} \\ $$$$\mathrm{1}−{a}=\mathrm{2}−\mathrm{2}{a}\:\Rightarrow\:{a}=\mathrm{1}\:\Rightarrow\:{b}=\mathrm{0} \\ $$$${y}=\mathrm{3}{x}^{\mathrm{2}} +{x} \\ $$$${t}_{{n}} =\left(\mathrm{3}{n}+\mathrm{1}\right){n} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 16/Mar/19
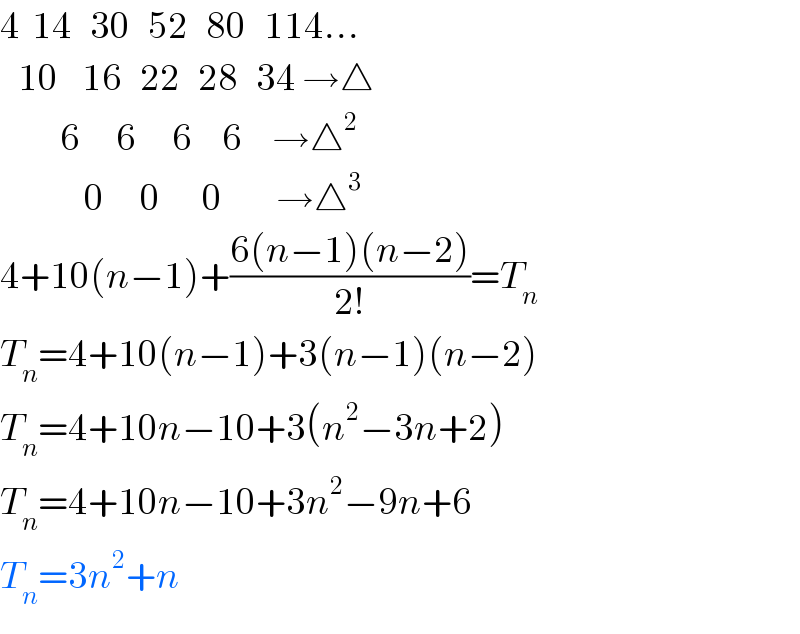
4 14 30 52 80 114... 10 16 22 28 34 →△ 6 6 6 6 →△^2 0 0 0 →△^3 4+10(n−1)+((6(n−1)(n−2))/(2!))=T_n T_n =4+10(n−1)+3(n−1)(n−2) T_n =4+10n−10+3(n^2 −3n+2) T_n =4+10n−10+3n^2 −9n+6 T_n =3n^2 +n
$$\mathrm{4}\:\:\mathrm{14}\:\:\:\mathrm{30}\:\:\:\mathrm{52}\:\:\:\mathrm{80}\:\:\:\mathrm{114}… \\ $$$$\:\:\:\mathrm{10}\:\:\:\:\mathrm{16}\:\:\:\mathrm{22}\:\:\:\mathrm{28}\:\:\:\mathrm{34}\:\rightarrow\bigtriangleup \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{6}\:\:\:\:\:\:\mathrm{6}\:\:\:\:\:\:\mathrm{6}\:\:\:\:\:\mathrm{6}\:\:\:\:\:\rightarrow\bigtriangleup^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\rightarrow\bigtriangleup^{\mathrm{3}} \\ $$$$\mathrm{4}+\mathrm{10}\left({n}−\mathrm{1}\right)+\frac{\mathrm{6}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)}{\mathrm{2}!}={T}_{{n}} \\ $$$${T}_{{n}} =\mathrm{4}+\mathrm{10}\left({n}−\mathrm{1}\right)+\mathrm{3}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right) \\ $$$${T}_{{n}} =\mathrm{4}+\mathrm{10}{n}−\mathrm{10}+\mathrm{3}\left({n}^{\mathrm{2}} −\mathrm{3}{n}+\mathrm{2}\right) \\ $$$${T}_{{n}} =\mathrm{4}+\mathrm{10}{n}−\mathrm{10}+\mathrm{3}{n}^{\mathrm{2}} −\mathrm{9}{n}+\mathrm{6} \\ $$$${T}_{{n}} =\mathrm{3}{n}^{\mathrm{2}} +{n} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *