Question Number 44128 by gunawan last updated on 22/Sep/18
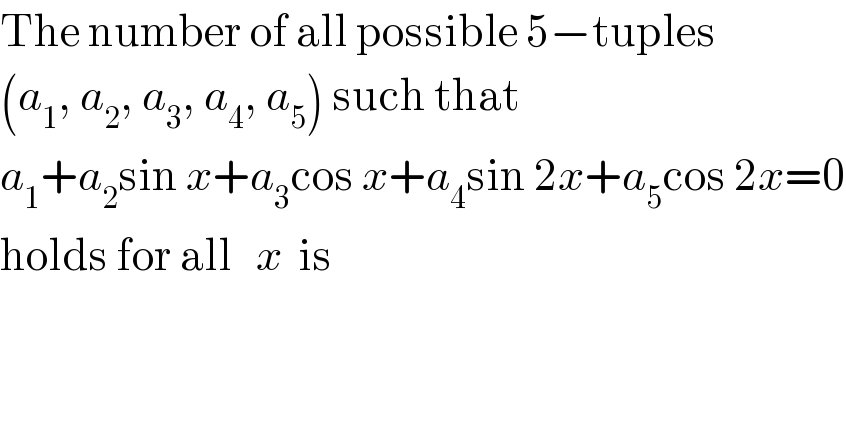
$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{all}\:\mathrm{possible}\:\mathrm{5}−\mathrm{tuples} \\ $$$$\left({a}_{\mathrm{1}} ,\:{a}_{\mathrm{2}} ,\:{a}_{\mathrm{3}} ,\:{a}_{\mathrm{4}} ,\:{a}_{\mathrm{5}} \right)\:\mathrm{such}\:\mathrm{that}\: \\ $$$${a}_{\mathrm{1}} +{a}_{\mathrm{2}} \mathrm{sin}\:{x}+{a}_{\mathrm{3}} \mathrm{cos}\:{x}+{a}_{\mathrm{4}} \mathrm{sin}\:\mathrm{2}{x}+{a}_{\mathrm{5}} \mathrm{cos}\:\mathrm{2}{x}=\mathrm{0} \\ $$$$\mathrm{holds}\:\mathrm{for}\:\mathrm{all}\:\:\:{x}\:\:\mathrm{is} \\ $$
Answered by MrW3 last updated on 22/Sep/18
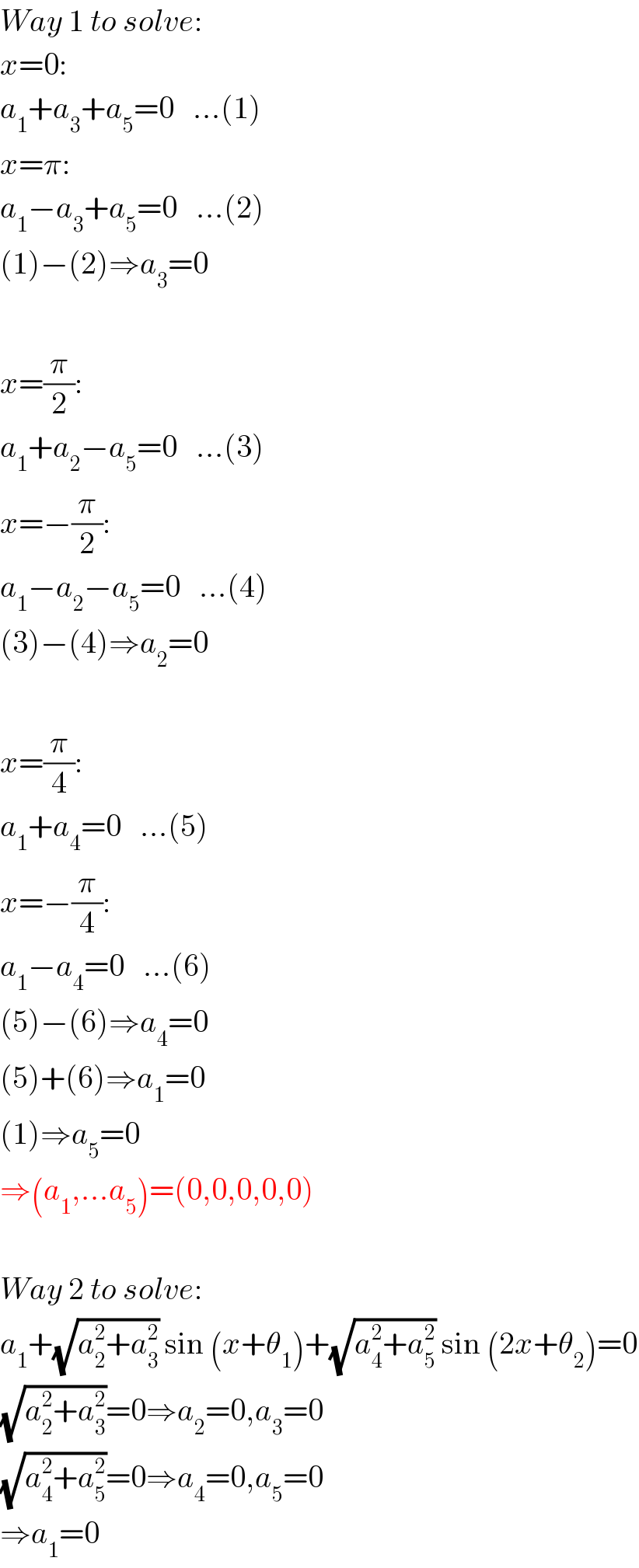
$${Way}\:\mathrm{1}\:{to}\:{solve}: \\ $$$${x}=\mathrm{0}: \\ $$$${a}_{\mathrm{1}} +{a}_{\mathrm{3}} +{a}_{\mathrm{5}} =\mathrm{0}\:\:\:…\left(\mathrm{1}\right) \\ $$$${x}=\pi: \\ $$$${a}_{\mathrm{1}} −{a}_{\mathrm{3}} +{a}_{\mathrm{5}} =\mathrm{0}\:\:\:…\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)−\left(\mathrm{2}\right)\Rightarrow{a}_{\mathrm{3}} =\mathrm{0} \\ $$$$ \\ $$$${x}=\frac{\pi}{\mathrm{2}}: \\ $$$${a}_{\mathrm{1}} +{a}_{\mathrm{2}} −{a}_{\mathrm{5}} =\mathrm{0}\:\:\:…\left(\mathrm{3}\right) \\ $$$${x}=−\frac{\pi}{\mathrm{2}}: \\ $$$${a}_{\mathrm{1}} −{a}_{\mathrm{2}} −{a}_{\mathrm{5}} =\mathrm{0}\:\:\:…\left(\mathrm{4}\right) \\ $$$$\left(\mathrm{3}\right)−\left(\mathrm{4}\right)\Rightarrow{a}_{\mathrm{2}} =\mathrm{0} \\ $$$$ \\ $$$${x}=\frac{\pi}{\mathrm{4}}: \\ $$$${a}_{\mathrm{1}} +{a}_{\mathrm{4}} =\mathrm{0}\:\:\:…\left(\mathrm{5}\right) \\ $$$${x}=−\frac{\pi}{\mathrm{4}}: \\ $$$${a}_{\mathrm{1}} −{a}_{\mathrm{4}} =\mathrm{0}\:\:\:…\left(\mathrm{6}\right) \\ $$$$\left(\mathrm{5}\right)−\left(\mathrm{6}\right)\Rightarrow{a}_{\mathrm{4}} =\mathrm{0} \\ $$$$\left(\mathrm{5}\right)+\left(\mathrm{6}\right)\Rightarrow{a}_{\mathrm{1}} =\mathrm{0} \\ $$$$\left(\mathrm{1}\right)\Rightarrow{a}_{\mathrm{5}} =\mathrm{0} \\ $$$$\Rightarrow\left({a}_{\mathrm{1}} ,…{a}_{\mathrm{5}} \right)=\left(\mathrm{0},\mathrm{0},\mathrm{0},\mathrm{0},\mathrm{0}\right) \\ $$$$ \\ $$$${Way}\:\mathrm{2}\:{to}\:{solve}: \\ $$$${a}_{\mathrm{1}} +\sqrt{{a}_{\mathrm{2}} ^{\mathrm{2}} +{a}_{\mathrm{3}} ^{\mathrm{2}} }\:\mathrm{sin}\:\left({x}+\theta_{\mathrm{1}} \right)+\sqrt{{a}_{\mathrm{4}} ^{\mathrm{2}} +{a}_{\mathrm{5}} ^{\mathrm{2}} }\:\mathrm{sin}\:\left(\mathrm{2}{x}+\theta_{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\sqrt{{a}_{\mathrm{2}} ^{\mathrm{2}} +{a}_{\mathrm{3}} ^{\mathrm{2}} }=\mathrm{0}\Rightarrow{a}_{\mathrm{2}} =\mathrm{0},{a}_{\mathrm{3}} =\mathrm{0} \\ $$$$\sqrt{{a}_{\mathrm{4}} ^{\mathrm{2}} +{a}_{\mathrm{5}} ^{\mathrm{2}} }=\mathrm{0}\Rightarrow{a}_{\mathrm{4}} =\mathrm{0},{a}_{\mathrm{5}} =\mathrm{0} \\ $$$$\Rightarrow{a}_{\mathrm{1}} =\mathrm{0} \\ $$
