Question Number 86496 by ram roop sharma last updated on 29/Mar/20
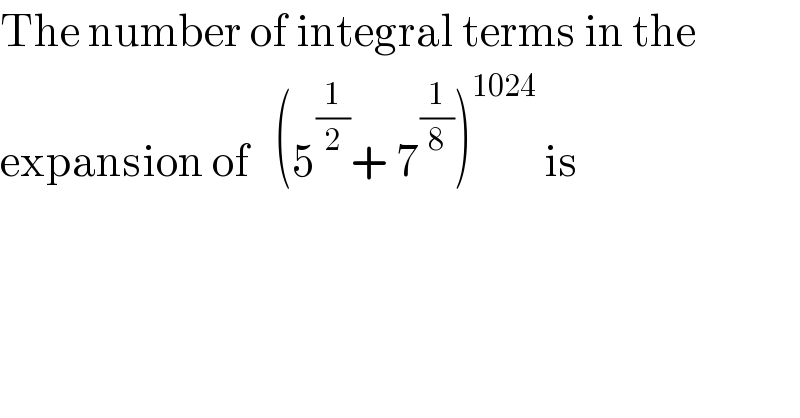
$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{integral}\:\mathrm{terms}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{expansion}\:\mathrm{of}\:\:\:\left(\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{2}}} +\:\mathrm{7}^{\frac{\mathrm{1}}{\mathrm{8}}} \right)^{\mathrm{1024}} \:\mathrm{is} \\ $$
Commented by Serlea last updated on 29/Mar/20

$$\mathrm{1025} \\ $$
Commented by mr W last updated on 29/Mar/20
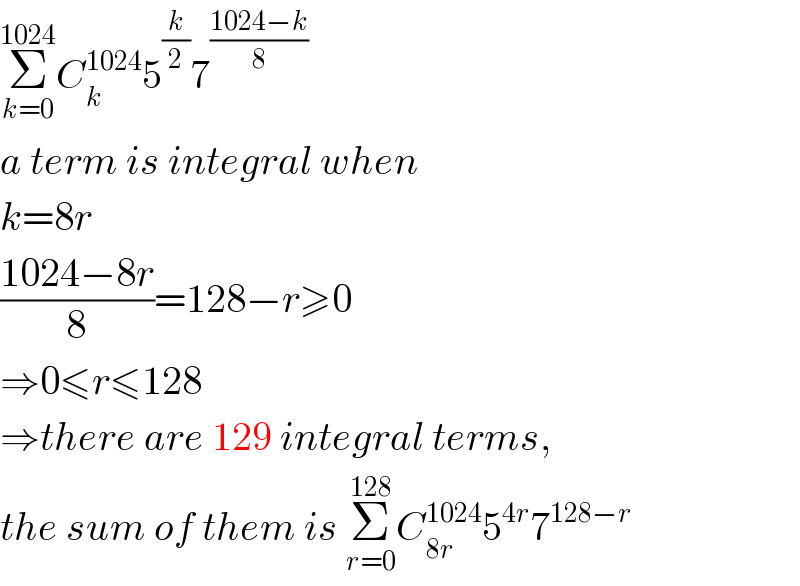
$$\underset{{k}=\mathrm{0}} {\overset{\mathrm{1024}} {\sum}}{C}_{{k}} ^{\mathrm{1024}} \mathrm{5}^{\frac{{k}}{\mathrm{2}}} \mathrm{7}^{\frac{\mathrm{1024}−{k}}{\mathrm{8}}} \\ $$$${a}\:{term}\:{is}\:{integral}\:{when} \\ $$$${k}=\mathrm{8}{r} \\ $$$$\frac{\mathrm{1024}−\mathrm{8}{r}}{\mathrm{8}}=\mathrm{128}−{r}\geqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{0}\leqslant{r}\leqslant\mathrm{128} \\ $$$$\Rightarrow{there}\:{are}\:\mathrm{129}\:{integral}\:{terms}, \\ $$$${the}\:{sum}\:{of}\:{them}\:{is}\:\underset{{r}=\mathrm{0}} {\overset{\mathrm{128}} {\sum}}{C}_{\mathrm{8}{r}} ^{\mathrm{1024}} \mathrm{5}^{\mathrm{4}{r}} \mathrm{7}^{\mathrm{128}−{r}} \\ $$
