Question Number 64414 by Yitagesuweldesenbet@gmail. Com last updated on 17/Jul/19
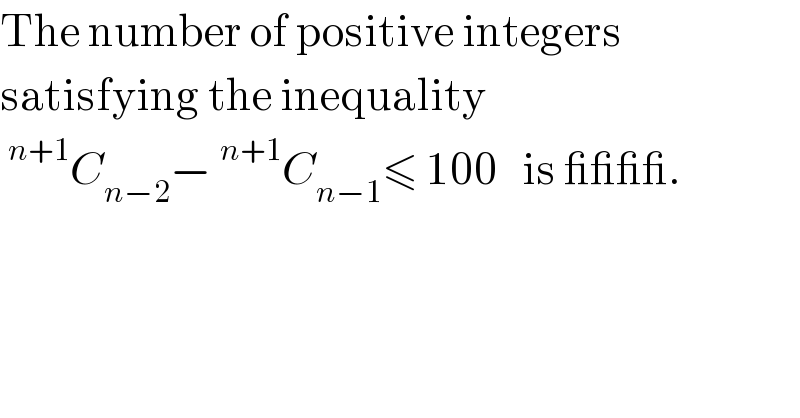
$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{positive}\:\mathrm{integers}\: \\ $$$$\mathrm{satisfying}\:\mathrm{the}\:\mathrm{inequality}\: \\ $$$$\:^{{n}+\mathrm{1}} {C}_{{n}−\mathrm{2}} −\:^{{n}+\mathrm{1}} {C}_{{n}−\mathrm{1}} \leqslant\:\mathrm{100}\:\:\:\mathrm{is}\:\_\_\_\_. \\ $$
Answered by mr W last updated on 17/Jul/19

$$\:^{{n}+\mathrm{1}} {C}_{{n}−\mathrm{2}} =\:^{{n}+\mathrm{1}} {C}_{\mathrm{3}} =\frac{\left({n}+\mathrm{1}\right){n}\left({n}−\mathrm{1}\right)}{\mathrm{3}!} \\ $$$$\:^{{n}+\mathrm{1}} {C}_{{n}−\mathrm{1}} =\:^{{n}+\mathrm{1}} {C}_{\mathrm{2}} =\frac{\left({n}+\mathrm{1}\right){n}}{\mathrm{2}!} \\ $$$$\frac{\left({n}+\mathrm{1}\right){n}\left({n}−\mathrm{1}\right)}{\mathrm{3}!}−\frac{\left({n}+\mathrm{1}\right){n}}{\mathrm{2}!}\leqslant\mathrm{100} \\ $$$$\left({n}+\mathrm{1}\right){n}\left({n}−\mathrm{4}\right)\leqslant\mathrm{600} \\ $$$${with}\:{n}=\mathrm{9}: \\ $$$${LHD}=\mathrm{10}×\mathrm{9}×\mathrm{5}=\mathrm{450}<\mathrm{600} \\ $$$${with}\:{n}=\mathrm{10}: \\ $$$${LHD}=\mathrm{11}×\mathrm{10}×\mathrm{6}=\mathrm{660}>\mathrm{600} \\ $$$$\Rightarrow\mathrm{2}\leqslant{n}\leqslant\mathrm{9} \\ $$
