Question Number 12841 by CheaV last updated on 04/May/17
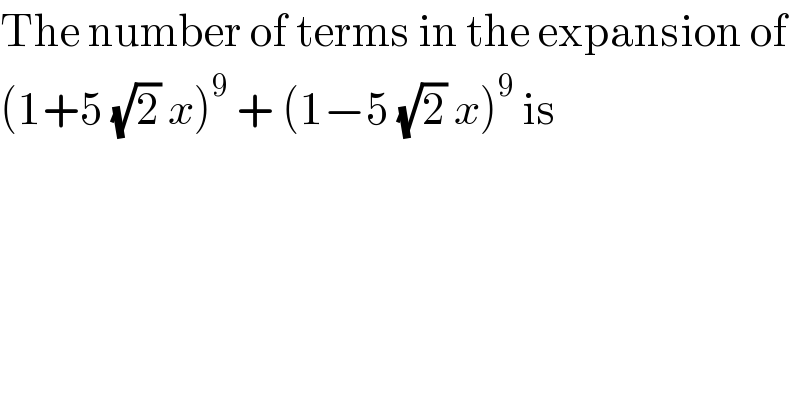
$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{terms}\:\mathrm{in}\:\mathrm{the}\:\mathrm{expansion}\:\mathrm{of} \\ $$$$\left(\mathrm{1}+\mathrm{5}\:\sqrt{\mathrm{2}}\:{x}\right)^{\mathrm{9}} \:+\:\left(\mathrm{1}−\mathrm{5}\:\sqrt{\mathrm{2}}\:{x}\right)^{\mathrm{9}} \:\mathrm{is} \\ $$
Answered by malwaan last updated on 04/May/17

$$\mathrm{5}\:\mathrm{terms} \\ $$
Answered by mrW1 last updated on 04/May/17
![(a+b)^n +(a−b)^n =Σ_(k=0) ^n C_k ^n a^(n−k) b^k +Σ_(k=0) ^n C_k ^n a^(n−k) (−b)^k =Σ_(k=0) ^n [1+(−1)^k ]C_k ^n a^(n−k) b^k =Σ_(k=0) ^n α^k C_k ^n a^k b^(n−k) with α^k =1+(−1)^k for n=9: α^k =2 if k=0,2,4,6,8 ⇒5 terms ≠0 α^k =0 if k=1,3,5,7,9 ⇒5 terms=0 ⇒Answer is 5 terms](https://www.tinkutara.com/question/Q12845.png)
$$\left({a}+{b}\right)^{{n}} +\left({a}−{b}\right)^{{n}} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{k}} ^{{n}} {a}^{{n}−{k}} {b}^{{k}} +\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{k}} ^{{n}} {a}^{{n}−{k}} \left(−{b}\right)^{{k}} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left[\mathrm{1}+\left(−\mathrm{1}\right)^{{k}} \right]{C}_{{k}} ^{{n}} {a}^{{n}−{k}} {b}^{{k}} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\alpha^{{k}} {C}_{{k}} ^{{n}} {a}^{{k}} {b}^{{n}−{k}} \\ $$$${with}\:\alpha^{{k}} =\mathrm{1}+\left(−\mathrm{1}\right)^{{k}} \\ $$$$ \\ $$$${for}\:{n}=\mathrm{9}: \\ $$$$\alpha^{{k}} =\mathrm{2}\:{if}\:{k}=\mathrm{0},\mathrm{2},\mathrm{4},\mathrm{6},\mathrm{8}\:\Rightarrow\mathrm{5}\:{terms}\:\neq\mathrm{0} \\ $$$$\alpha^{{k}} =\mathrm{0}\:{if}\:{k}=\mathrm{1},\mathrm{3},\mathrm{5},\mathrm{7},\mathrm{9}\:\Rightarrow\mathrm{5}\:{terms}=\mathrm{0} \\ $$$$ \\ $$$$\Rightarrow{Answer}\:{is}\:\mathrm{5}\:{terms} \\ $$
