Question Number 44231 by Mawitea Cck last updated on 24/Sep/18
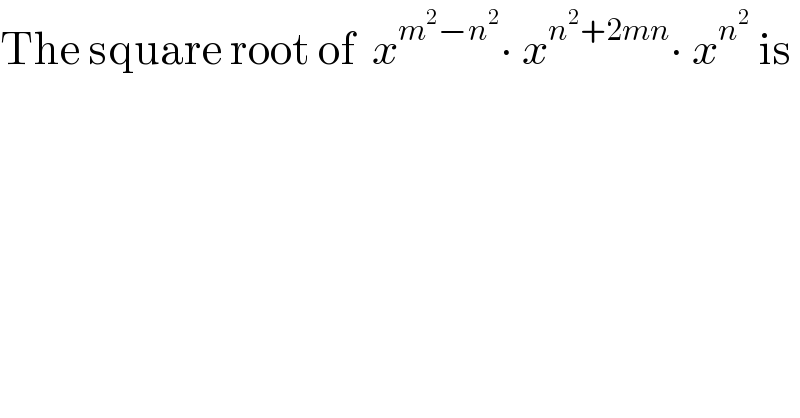
$$\mathrm{The}\:\mathrm{square}\:\mathrm{root}\:\mathrm{of}\:\:{x}^{{m}^{\mathrm{2}} −{n}^{\mathrm{2}} } \centerdot\:{x}^{{n}^{\mathrm{2}} +\mathrm{2}{mn}} \centerdot\:{x}^{{n}^{\mathrm{2}} } \:\mathrm{is} \\ $$
Answered by Joel578 last updated on 24/Sep/18
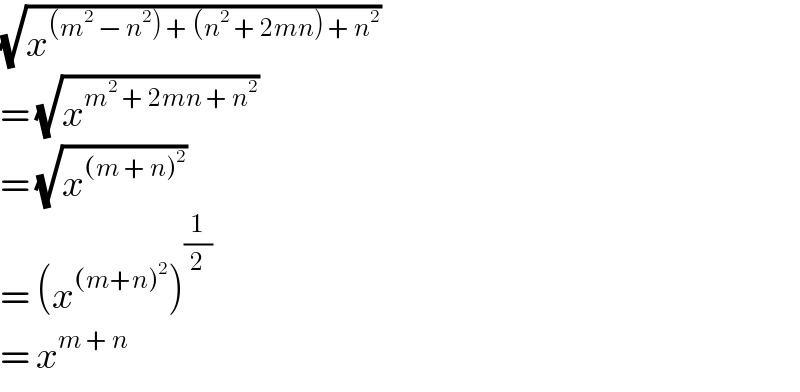
$$\sqrt{{x}^{\left({m}^{\mathrm{2}} \:−\:{n}^{\mathrm{2}} \right)\:+\:\left({n}^{\mathrm{2}} \:+\:\mathrm{2}{mn}\right)\:+\:{n}^{\mathrm{2}} } }\: \\ $$$$=\:\sqrt{{x}^{{m}^{\mathrm{2}} \:+\:\mathrm{2}{mn}\:+\:{n}^{\mathrm{2}} } } \\ $$$$=\:\sqrt{{x}^{\left({m}\:+\:{n}\right)^{\mathrm{2}} } } \\ $$$$=\:\left({x}^{\left({m}+{n}\right)^{\mathrm{2}} } \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\:{x}^{{m}\:+\:{n}} \\ $$
