Question Number 92003 by zainal tanjung last updated on 04/May/20
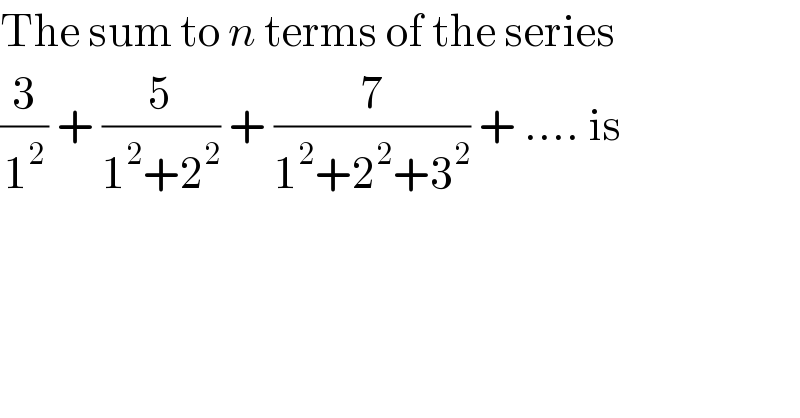
$$\mathrm{The}\:\mathrm{sum}\:\mathrm{to}\:{n}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{the}\:\mathrm{series} \\ $$$$\frac{\mathrm{3}}{\mathrm{1}^{\mathrm{2}} }\:+\:\frac{\mathrm{5}}{\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }\:+\:\frac{\mathrm{7}}{\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} }\:+\:….\:\mathrm{is} \\ $$
Commented by Prithwish Sen 1 last updated on 04/May/20
![t_(n ) = ((6(2n+1))/(n(n+1)(2n+1))) = 6[(1/n)−(1/(n+1))] now the series becomes lim_(k→∞) 6[Σ_(n=1) ^k ((1/n)−(1/(n+1)))] = lim_(k→∞) 6[(k/(k+1))]= lim_(k→∞) 6.(1/(1+(1/k))) = 6.1 = 6 please check](https://www.tinkutara.com/question/Q92011.png)
$$\mathrm{t}_{\mathrm{n}\:} \:=\:\frac{\mathrm{6}\left(\mathrm{2n}+\mathrm{1}\right)}{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{2n}+\mathrm{1}\right)}\:=\:\mathrm{6}\left[\frac{\mathrm{1}}{\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\right] \\ $$$$\mathrm{now}\:\mathrm{the}\:\mathrm{series}\:\mathrm{becomes} \\ $$$$\underset{\mathrm{k}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{6}\left[\underset{\mathrm{n}=\mathrm{1}} {\overset{\mathrm{k}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\right)\right]\:=\:\underset{\mathrm{k}\rightarrow\infty} {\mathrm{lim}}\:\:\mathrm{6}\left[\frac{\mathrm{k}}{\mathrm{k}+\mathrm{1}}\right]= \\ $$$$\underset{\mathrm{k}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{6}.\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{k}}}\:\:=\:\mathrm{6}.\mathrm{1}\:=\:\mathrm{6}\:\:\:\:\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}} \\ $$
Commented by mathmax by abdo last updated on 04/May/20
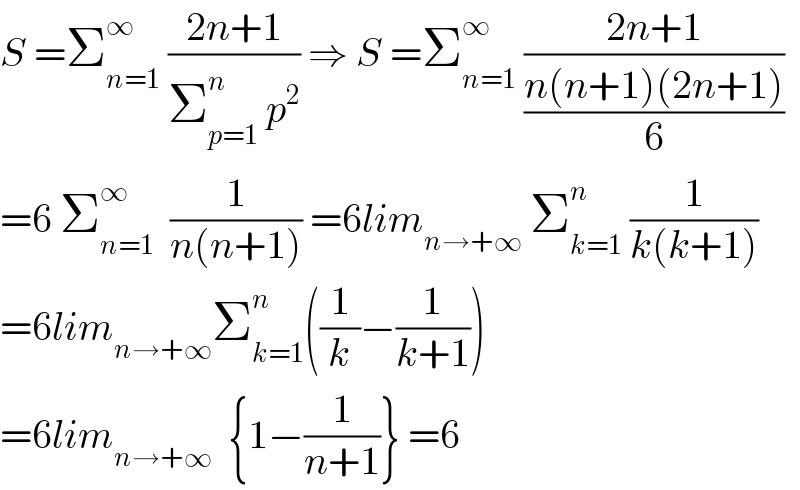
$${S}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{2}{n}+\mathrm{1}}{\sum_{{p}=\mathrm{1}} ^{{n}} \:{p}^{\mathrm{2}} }\:\Rightarrow\:{S}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{2}{n}+\mathrm{1}}{\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}} \\ $$$$=\mathrm{6}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)}\:=\mathrm{6}{lim}_{{n}\rightarrow+\infty} \:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}\left({k}+\mathrm{1}\right)} \\ $$$$=\mathrm{6}{lim}_{{n}\rightarrow+\infty} \sum_{{k}=\mathrm{1}} ^{{n}} \left(\frac{\mathrm{1}}{{k}}−\frac{\mathrm{1}}{{k}+\mathrm{1}}\right) \\ $$$$=\mathrm{6}{lim}_{{n}\rightarrow+\infty} \:\:\left\{\mathrm{1}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right\}\:=\mathrm{6} \\ $$
