The-system-of-equations-kx-y-z-1-x-ky-z-k-and-x-y-kz-k-2-have-no-solution-if-k-equals-

Question Number 88872 by Zainal Arifin last updated on 13/Apr/20

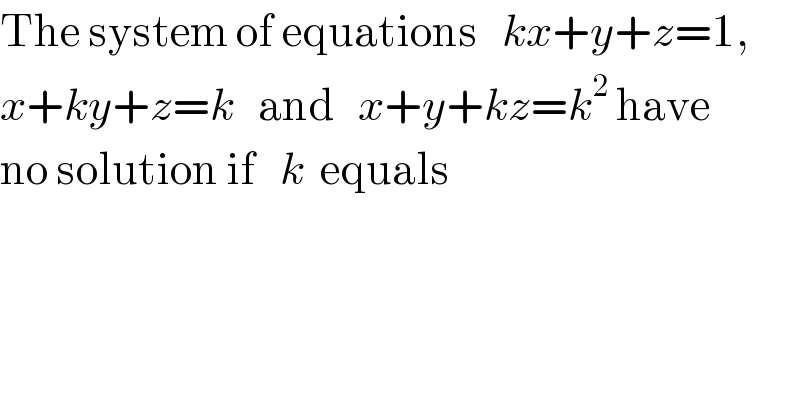
The system of equations k x + y + z = 1,

x + k y + z = k and x + y + k z = k^{2} have

no solution if k equals

Commented by john santu last updated on 13/Apr/20

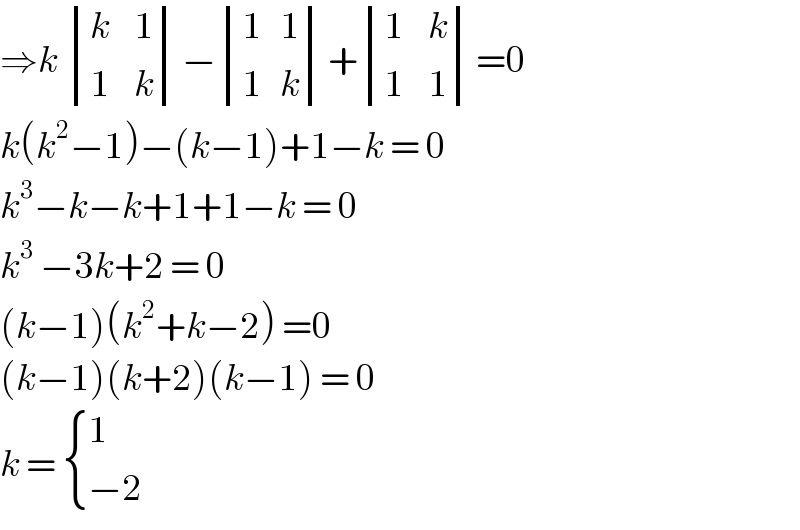
\Rightarrow k | \begin{matrix} k 1 \\ 1 k \end{matrix} | - | \begin{matrix} 1 1 \\ 1 k \end{matrix} | + | \begin{matrix} 1 k \\ 1 1 \end{matrix} | = 0

k (k^{2} - 1) - (k - 1) + 1 - k = 0

k^{3} - k - k + 1 + 1 - k = 0

k^{3} - 3 k + 2 = 0

(k - 1) (k^{2} + k - 2) = 0

(k - 1) (k + 2) (k - 1) = 0

k = {\begin{cases} 1 \\ - 2 \end{cases}