Question Number 8050 by Chantria last updated on 28/Sep/16

$$\mathrm{The}\:\mathrm{value}\:\mathrm{of} \\ $$$$\frac{\mathrm{18}^{\mathrm{3}} +\mathrm{7}^{\mathrm{3}} +\mathrm{3}\:\centerdot\:\mathrm{18}\:\centerdot\:\mathrm{7}\:\centerdot\:\mathrm{25}}{\mathrm{3}^{\mathrm{6}} +\mathrm{6}\centerdot\mathrm{243}\centerdot\mathrm{2}+\mathrm{15}\centerdot\mathrm{181}\centerdot\mathrm{4}+\mathrm{20}\centerdot\mathrm{27}\centerdot\mathrm{8}+\mathrm{15}\centerdot\mathrm{9}\centerdot\mathrm{16}+\mathrm{6}\centerdot\mathrm{3}\centerdot\mathrm{32}+\mathrm{64}} \\ $$$$\mathrm{is} \\ $$
Answered by sandy_suhendra last updated on 28/Sep/16
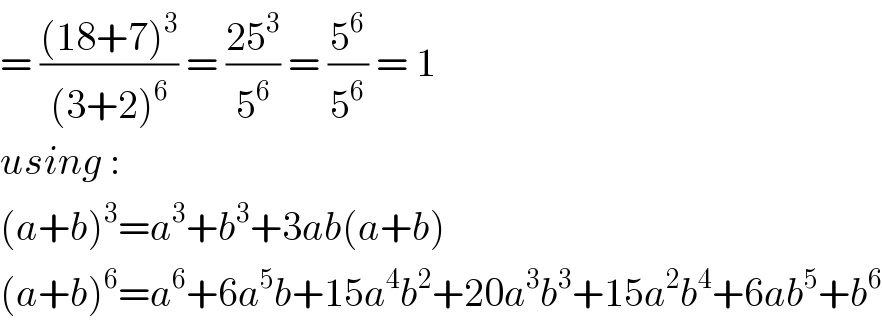
$$=\:\frac{\left(\mathrm{18}+\mathrm{7}\right)^{\mathrm{3}} }{\left(\mathrm{3}+\mathrm{2}\right)^{\mathrm{6}} }\:=\:\frac{\mathrm{25}^{\mathrm{3}} }{\mathrm{5}^{\mathrm{6}} }\:=\:\frac{\mathrm{5}^{\mathrm{6}} }{\mathrm{5}^{\mathrm{6}} }\:=\:\mathrm{1} \\ $$$${using}\:: \\ $$$$\left({a}+{b}\right)^{\mathrm{3}} ={a}^{\mathrm{3}} +{b}^{\mathrm{3}} +\mathrm{3}{ab}\left({a}+{b}\right) \\ $$$$\left({a}+{b}\right)^{\mathrm{6}} ={a}^{\mathrm{6}} +\mathrm{6}{a}^{\mathrm{5}} {b}+\mathrm{15}{a}^{\mathrm{4}} {b}^{\mathrm{2}} +\mathrm{20}{a}^{\mathrm{3}} {b}^{\mathrm{3}} +\mathrm{15}{a}^{\mathrm{2}} {b}^{\mathrm{4}} +\mathrm{6}{ab}^{\mathrm{5}} +{b}^{\mathrm{6}} \\ $$
