Question Number 48528 by Pk1167156@gmail.com last updated on 25/Nov/18
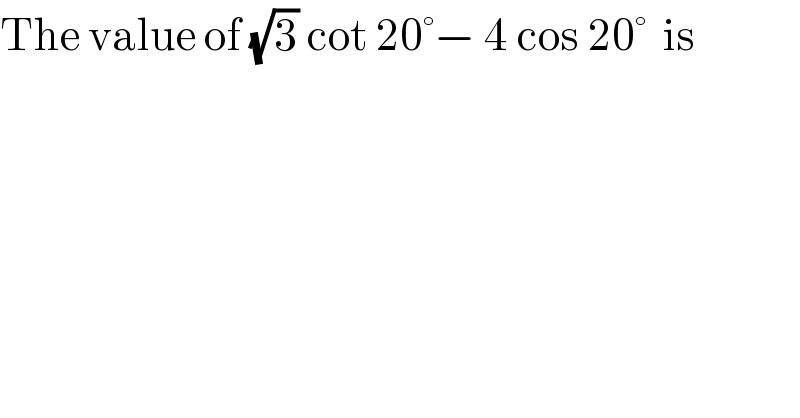
$$\mathrm{The}\:\mathrm{value}\:\mathrm{of}\:\sqrt{\mathrm{3}}\:\mathrm{cot}\:\mathrm{20}°−\:\mathrm{4}\:\mathrm{cos}\:\mathrm{20}°\:\:\mathrm{is} \\ $$
Answered by math1967 last updated on 25/Nov/18
![(((√3)cos20−4cos20sin20)/(sin20)) =((tan60cos20−2sin40)/(sin20)) =((((sin60cos20)/(cos60))−2sin40)/(sin20)) =((2sin60cos 20−2sin40)/(sin20)) [(1/(cos60))=2] =((sin(60+20)+sin (60−20)−2sin 40)/(sin 20)) =((sin80−sin40)/(sin20))=((2sin20cos60)/(sin 20))=1Ans](https://www.tinkutara.com/question/Q48554.png)
$$\:\frac{\sqrt{\mathrm{3}}{cos}\mathrm{20}−\mathrm{4}{cos}\mathrm{20}{sin}\mathrm{20}}{{sin}\mathrm{20}}\:\:\: \\ $$$$=\frac{{tan}\mathrm{60}{cos}\mathrm{20}−\mathrm{2}{sin}\mathrm{40}}{{sin}\mathrm{20}} \\ $$$$=\frac{\frac{{sin}\mathrm{60}{cos}\mathrm{20}}{{cos}\mathrm{60}}−\mathrm{2}{sin}\mathrm{40}}{{sin}\mathrm{20}} \\ $$$$=\frac{\mathrm{2}{sin}\mathrm{60cos}\:\mathrm{20}−\mathrm{2}{sin}\mathrm{40}}{{sin}\mathrm{20}}\:\:\left[\frac{\mathrm{1}}{{cos}\mathrm{60}}=\mathrm{2}\right] \\ $$$$=\frac{{sin}\left(\mathrm{60}+\mathrm{20}\right)+\mathrm{sin}\:\left(\mathrm{60}−\mathrm{20}\right)−\mathrm{2sin}\:\mathrm{40}}{\mathrm{sin}\:\mathrm{20}} \\ $$$$=\frac{{sin}\mathrm{80}−{sin}\mathrm{40}}{{sin}\mathrm{20}}=\frac{\mathrm{2}{sin}\mathrm{20}{cos}\mathrm{60}}{\mathrm{sin}\:\mathrm{20}}=\mathrm{1}{Ans} \\ $$$$ \\ $$
