Question Number 49751 by Pk1167156@gmail.com last updated on 10/Dec/18
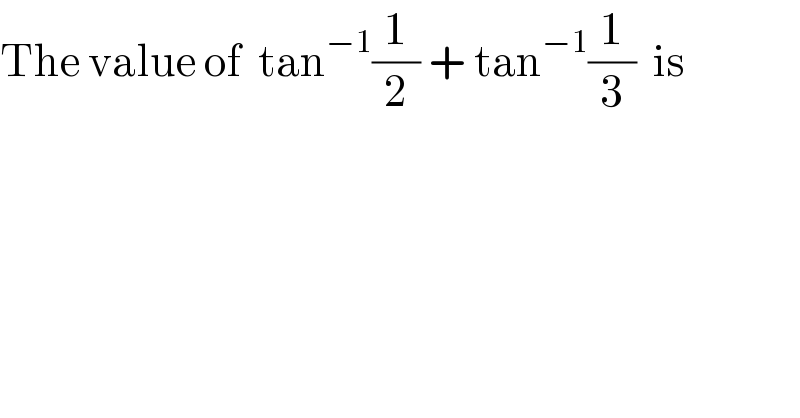
$$\mathrm{The}\:\mathrm{value}\:\mathrm{of}\:\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}\:+\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{3}}\:\:\mathrm{is} \\ $$
Commented by maxmathsup by imad last updated on 10/Dec/18
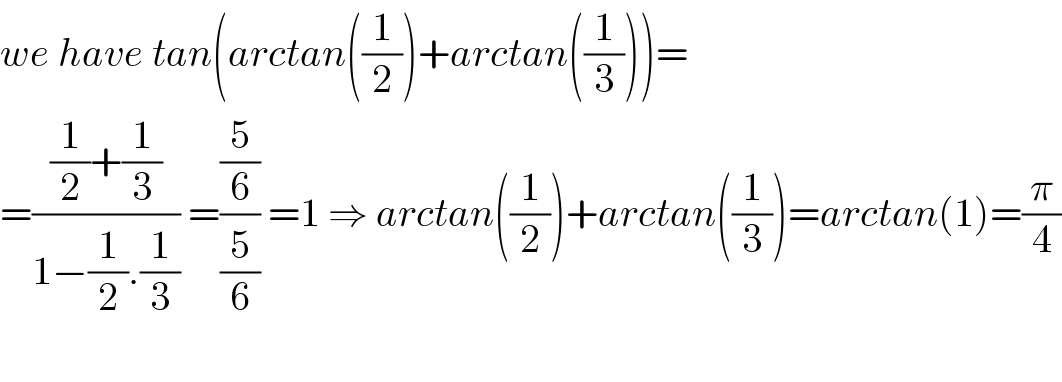
$${we}\:{have}\:{tan}\left({arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+{arctan}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right)= \\ $$$$=\frac{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{3}}}\:=\frac{\frac{\mathrm{5}}{\mathrm{6}}}{\frac{\mathrm{5}}{\mathrm{6}}}\:=\mathrm{1}\:\Rightarrow\:{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+{arctan}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)={arctan}\left(\mathrm{1}\right)=\frac{\pi}{\mathrm{4}} \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 10/Dec/18
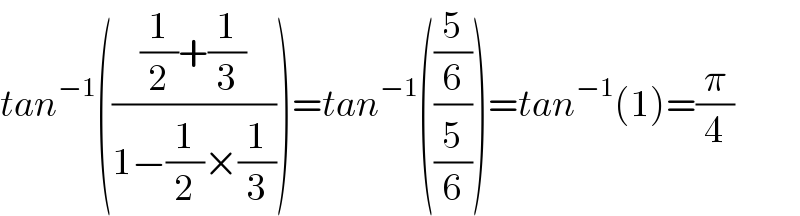
$${tan}^{−\mathrm{1}} \left(\frac{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{3}}}\right)={tan}^{−\mathrm{1}} \left(\frac{\frac{\mathrm{5}}{\mathrm{6}}}{\frac{\mathrm{5}}{\mathrm{6}}}\right)={tan}^{−\mathrm{1}} \left(\mathrm{1}\right)=\frac{\pi}{\mathrm{4}} \\ $$
