Question Number 79437 by Vishal Sharma last updated on 25/Jan/20
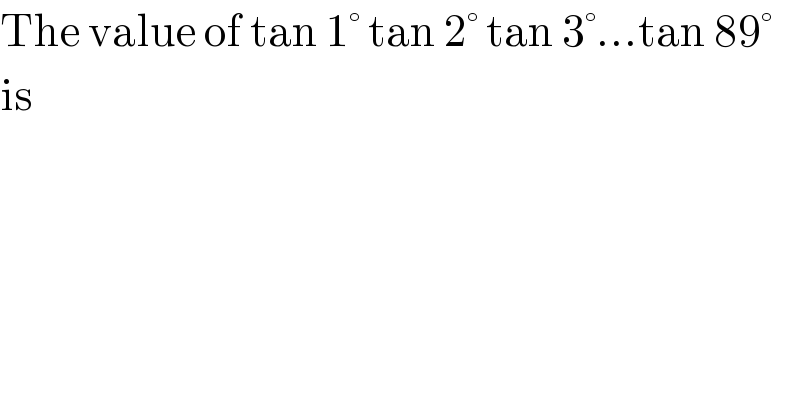
$$\mathrm{The}\:\mathrm{value}\:\mathrm{of}\:\mathrm{tan}\:\mathrm{1}°\:\mathrm{tan}\:\mathrm{2}°\:\mathrm{tan}\:\mathrm{3}°…\mathrm{tan}\:\mathrm{89}° \\ $$$$\mathrm{is} \\ $$
Commented by mr W last updated on 25/Jan/20
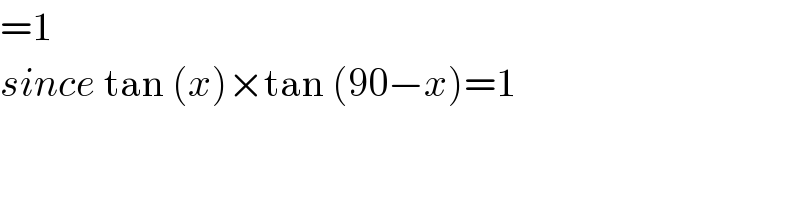
$$=\mathrm{1} \\ $$$${since}\:\mathrm{tan}\:\left({x}\right)×\mathrm{tan}\:\left(\mathrm{90}−{x}\right)=\mathrm{1} \\ $$
Commented by mathmax by abdo last updated on 25/Jan/20
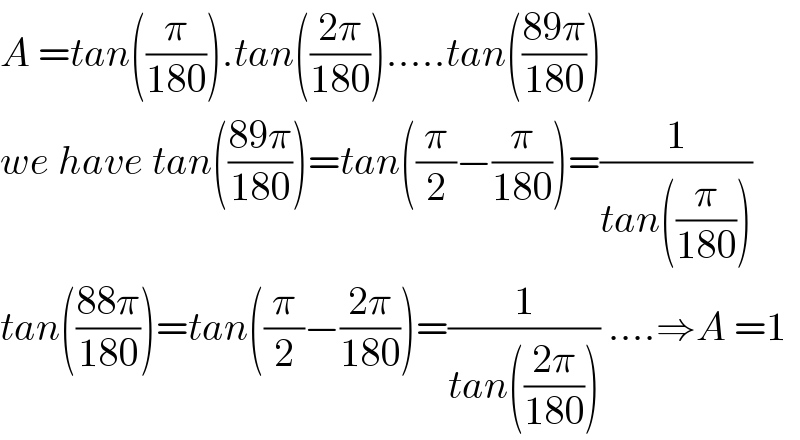
$${A}\:={tan}\left(\frac{\pi}{\mathrm{180}}\right).{tan}\left(\frac{\mathrm{2}\pi}{\mathrm{180}}\right)…..{tan}\left(\frac{\mathrm{89}\pi}{\mathrm{180}}\right) \\ $$$${we}\:{have}\:{tan}\left(\frac{\mathrm{89}\pi}{\mathrm{180}}\right)={tan}\left(\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{180}}\right)=\frac{\mathrm{1}}{{tan}\left(\frac{\pi}{\mathrm{180}}\right)} \\ $$$${tan}\left(\frac{\mathrm{88}\pi}{\mathrm{180}}\right)={tan}\left(\frac{\pi}{\mathrm{2}}−\frac{\mathrm{2}\pi}{\mathrm{180}}\right)=\frac{\mathrm{1}}{{tan}\left(\frac{\mathrm{2}\pi}{\mathrm{180}}\right)}\:….\Rightarrow{A}\:=\mathrm{1} \\ $$
