Question Number 57138 by mustakim420 last updated on 30/Mar/19
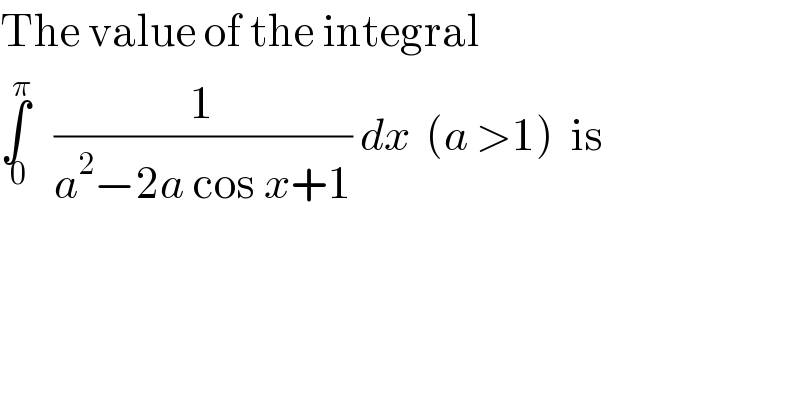
$$\mathrm{The}\:\mathrm{value}\:\mathrm{of}\:\mathrm{the}\:\mathrm{integral} \\ $$$$\underset{\:\mathrm{0}} {\overset{\pi} {\int}}\:\:\:\frac{\mathrm{1}}{{a}^{\mathrm{2}} −\mathrm{2}{a}\:\mathrm{cos}\:{x}+\mathrm{1}}\:{dx}\:\:\left({a}\:>\mathrm{1}\right)\:\:\mathrm{is} \\ $$
Commented by maxmathsup by imad last updated on 30/Mar/19
![let f(a) =∫_0 ^π (dx/(a^2 −2acosx +1)) ⇒f(a) =_(tan((x/2))=t) ∫_0 ^(+∞) ((2dt)/((1+t^2 )(a^2 −2a((1−t^2 )/(1+t^2 )) +1))) =2 ∫_0 ^∞ (dt/((1+t^2 )a^2 −2a(1−t^2 )+1+t^2 )) =2 ∫_0 ^∞ (dt/(a^2 t^2 +a^2 −2a+2at^2 +1+t^2 )) =2 ∫_0 ^∞ (dt/((a^2 +2a+1)t^(2 ) +a^2 −2a+1)) =2 ∫_0 ^∞ (dt/((a+1)^2 t^2 +(a−1)^2 )) changement (a+1)t =(a−1)u give f(a) =2 ∫_0 ^∞ (1/((a−1)^2 (1+u^2 ))) ((a−1)/(a+1)) du =(2/(a^2 −1)) [arctan(u)]_0 ^(+∞) =(2/(a^2 −1)) (π/2) =(π/(a^2 −1)) ⇒f(a) =(π/(a^2 −1)) with a>1 .](https://www.tinkutara.com/question/Q57156.png)
$${let}\:\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\pi} \:\:\:\:\:\frac{{dx}}{{a}^{\mathrm{2}} −\mathrm{2}{acosx}\:+\mathrm{1}}\:\Rightarrow{f}\left({a}\right)\:=_{{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}} \:\:\int_{\mathrm{0}} ^{+\infty} \:\:\:\frac{\mathrm{2}{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left({a}^{\mathrm{2}} \:−\mathrm{2}{a}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\:+\mathrm{1}\right)} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right){a}^{\mathrm{2}} \:−\mathrm{2}{a}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)+\mathrm{1}+{t}^{\mathrm{2}} }\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{{a}^{\mathrm{2}} {t}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \:−\mathrm{2}{a}+\mathrm{2}{at}^{\mathrm{2}} \:+\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{\left({a}^{\mathrm{2}} \:+\mathrm{2}{a}+\mathrm{1}\right){t}^{\mathrm{2}\:} \:+{a}^{\mathrm{2}} −\mathrm{2}{a}+\mathrm{1}}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{dt}}{\left({a}+\mathrm{1}\right)^{\mathrm{2}} {t}^{\mathrm{2}} \:+\left({a}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${changement}\:\left({a}+\mathrm{1}\right){t}\:=\left({a}−\mathrm{1}\right){u}\:\:{give} \\ $$$${f}\left({a}\right)\:=\mathrm{2}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{\mathrm{1}}{\left({a}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:\frac{{a}−\mathrm{1}}{{a}+\mathrm{1}}\:{du}\:=\frac{\mathrm{2}}{{a}^{\mathrm{2}} −\mathrm{1}}\:\left[{arctan}\left({u}\right)\right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\frac{\mathrm{2}}{{a}^{\mathrm{2}} −\mathrm{1}}\:\frac{\pi}{\mathrm{2}}\:=\frac{\pi}{{a}^{\mathrm{2}} −\mathrm{1}}\:\:\Rightarrow{f}\left({a}\right)\:=\frac{\pi}{{a}^{\mathrm{2}} \:−\mathrm{1}}\:\:{with}\:{a}>\mathrm{1}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 30/Mar/19
![∫(dx/(a^2 +1−2acosx)) (1/(2a))∫(dx/(k−cosx)) [k=((a^2 +1)/(2a))] t=tan(x/2) 2dt=sec^2 (x/2)dx dx=((2dt)/(1+t^2 )) (1/(2a))∫((2dt)/((1+t^2 )(k−((1−t^2 )/(1+t^2 ))))) (1/a)∫(dt/(k+kt^2 −1+t^2 )) (1/a)∫(dt/((k−1)+t^2 (k+1))) (1/(a(k+1)))∫(dt/(((k−1)/(k+1))+t^2 )) (1/(a(((a^2 +1)/(2a))+1)))×(1/( (√((k−1)/(k+1)))))tan^(−1) ((t/( (√((k−1)/(k+1)))))) k=((a^2 +1)/(2a)) ((k−1)/(k+1))=((a^2 +1+2a)/(a^2 +1−2a))=(((a+1)^2 )/((a−1)^2 )) (√((k−1)/(k+1))) =((a+1)/(a−1)) (2/((a+1)^2 ))×(1/((a−1)/(a+1)))∣tan^(−1) (((tan(x/2))/((a−1)/(a+1))))∣_0 ^π (2/(a^2 −1))×[tan^(−1) (∞)−0] (2/(a^2 −1))×(π/2)→(π/(a^2 −1))](https://www.tinkutara.com/question/Q57145.png)
$$\int\frac{{dx}}{{a}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{acosx}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{a}}\int\frac{{dx}}{{k}−{cosx}}\:\:\left[{k}=\frac{{a}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{a}}\right] \\ $$$${t}={tan}\frac{{x}}{\mathrm{2}}\:\:\:\:\:\:\mathrm{2}{dt}={sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}{dx} \\ $$$${dx}=\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{a}}\int\frac{\mathrm{2}{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left({k}−\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)} \\ $$$$\frac{\mathrm{1}}{{a}}\int\frac{{dt}}{{k}+{kt}^{\mathrm{2}} −\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{{a}}\int\frac{{dt}}{\left({k}−\mathrm{1}\right)+{t}^{\mathrm{2}} \left({k}+\mathrm{1}\right)} \\ $$$$\frac{\mathrm{1}}{{a}\left({k}+\mathrm{1}\right)}\int\frac{{dt}}{\frac{{k}−\mathrm{1}}{{k}+\mathrm{1}}+{t}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{{a}\left(\frac{{a}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{a}}+\mathrm{1}\right)}×\frac{\mathrm{1}}{\:\sqrt{\frac{{k}−\mathrm{1}}{{k}+\mathrm{1}}}}{tan}^{−\mathrm{1}} \left(\frac{{t}}{\:\sqrt{\frac{{k}−\mathrm{1}}{{k}+\mathrm{1}}}}\right) \\ $$$$ \\ $$$${k}=\frac{{a}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{a}} \\ $$$$\frac{{k}−\mathrm{1}}{{k}+\mathrm{1}}=\frac{{a}^{\mathrm{2}} +\mathrm{1}+\mathrm{2}{a}}{{a}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{a}}=\frac{\left({a}+\mathrm{1}\right)^{\mathrm{2}} }{\left({a}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\sqrt{\frac{{k}−\mathrm{1}}{{k}+\mathrm{1}}}\:=\frac{{a}+\mathrm{1}}{{a}−\mathrm{1}} \\ $$$$\frac{\mathrm{2}}{\left({a}+\mathrm{1}\right)^{\mathrm{2}} }×\frac{\mathrm{1}}{\frac{{a}−\mathrm{1}}{{a}+\mathrm{1}}}\mid{tan}^{−\mathrm{1}} \left(\frac{{tan}\frac{{x}}{\mathrm{2}}}{\frac{{a}−\mathrm{1}}{{a}+\mathrm{1}}}\right)\mid_{\mathrm{0}} ^{\pi} \\ $$$$\frac{\mathrm{2}}{{a}^{\mathrm{2}} −\mathrm{1}}×\left[{tan}^{−\mathrm{1}} \left(\infty\right)−\mathrm{0}\right] \\ $$$$\frac{\mathrm{2}}{{a}^{\mathrm{2}} −\mathrm{1}}×\frac{\pi}{\mathrm{2}}\rightarrow\frac{\pi}{{a}^{\mathrm{2}} −\mathrm{1}} \\ $$
