Question Number 91494 by Zainal Arifin last updated on 01/May/20
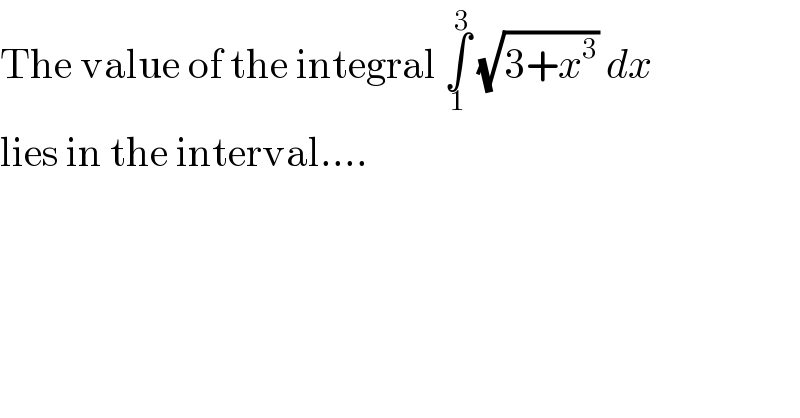
$$\mathrm{The}\:\mathrm{value}\:\mathrm{of}\:\mathrm{the}\:\mathrm{integral}\:\underset{\:\mathrm{1}} {\overset{\mathrm{3}} {\int}}\:\sqrt{\mathrm{3}+{x}^{\mathrm{3}} }\:{dx} \\ $$$$\mathrm{lies}\:\mathrm{in}\:\mathrm{the}\:\mathrm{interval}…. \\ $$
Answered by Joel578 last updated on 01/May/20
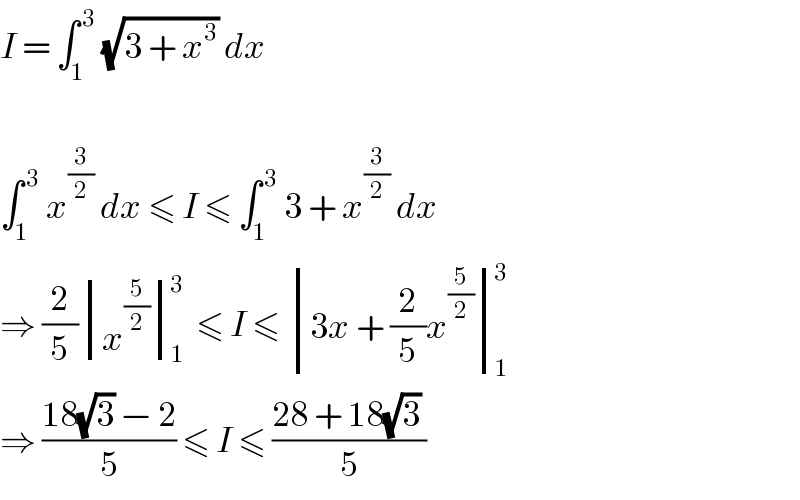
$${I}\:=\:\int_{\mathrm{1}} ^{\:\mathrm{3}} \:\sqrt{\mathrm{3}\:+\:{x}^{\mathrm{3}} }\:{dx} \\ $$$$ \\ $$$$\int_{\mathrm{1}} ^{\:\mathrm{3}} \:{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \:{dx}\:\leqslant\:{I}\:\leqslant\:\int_{\mathrm{1}} ^{\:\mathrm{3}} \:\mathrm{3}\:+\:{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \:{dx} \\ $$$$\Rightarrow\:\frac{\mathrm{2}}{\mathrm{5}}\begin{vmatrix}{{x}^{\frac{\mathrm{5}}{\mathrm{2}}} }\end{vmatrix}_{\mathrm{1}} ^{\mathrm{3}} \:\leqslant\:{I}\:\leqslant\:\begin{vmatrix}{\mathrm{3}{x}\:+\:\frac{\mathrm{2}}{\mathrm{5}}{x}^{\frac{\mathrm{5}}{\mathrm{2}}} }\end{vmatrix}_{\mathrm{1}} ^{\mathrm{3}} \\ $$$$\Rightarrow\:\frac{\mathrm{18}\sqrt{\mathrm{3}}\:−\:\mathrm{2}}{\mathrm{5}}\:\leqslant\:{I}\:\leqslant\:\frac{\mathrm{28}\:+\:\mathrm{18}\sqrt{\mathrm{3}}\:}{\mathrm{5}}\: \\ $$
