Menu Close

The-value-of-the-sum-of-the-series-3-n-C-0-8-n-C-1-13-n-C-2-18-n-C-3-1-n-3-5n-n-C-n-

Tinku Tara 0 Comments
Pin




Question Number 8156 by 314159 last updated on 02/Oct/16
The value of the sum of the series 3^n C_0 − 8^n C_1 +13^n C_2 −18^n C_3 +...+(−1)^n (3+5n)^n C_n ]
$$\mathrm{The}\:\mathrm{value}\:\mathrm{of}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{series} \\ $$$$\left.\mathrm{3}\:^{{n}} {C}_{\mathrm{0}} −\:\mathrm{8}\:^{{n}} {C}_{\mathrm{1}} +\mathrm{13}\:^{{n}} {C}_{\mathrm{2}} −\mathrm{18}\:^{{n}} {C}_{\mathrm{3}} +…+\left(−\mathrm{1}\right)^{{n}} \:\left(\mathrm{3}+\mathrm{5}{n}\right)\:^{{n}} {C}_{{n}} \right] \\ $$
Commented by Yozzias last updated on 02/Oct/16
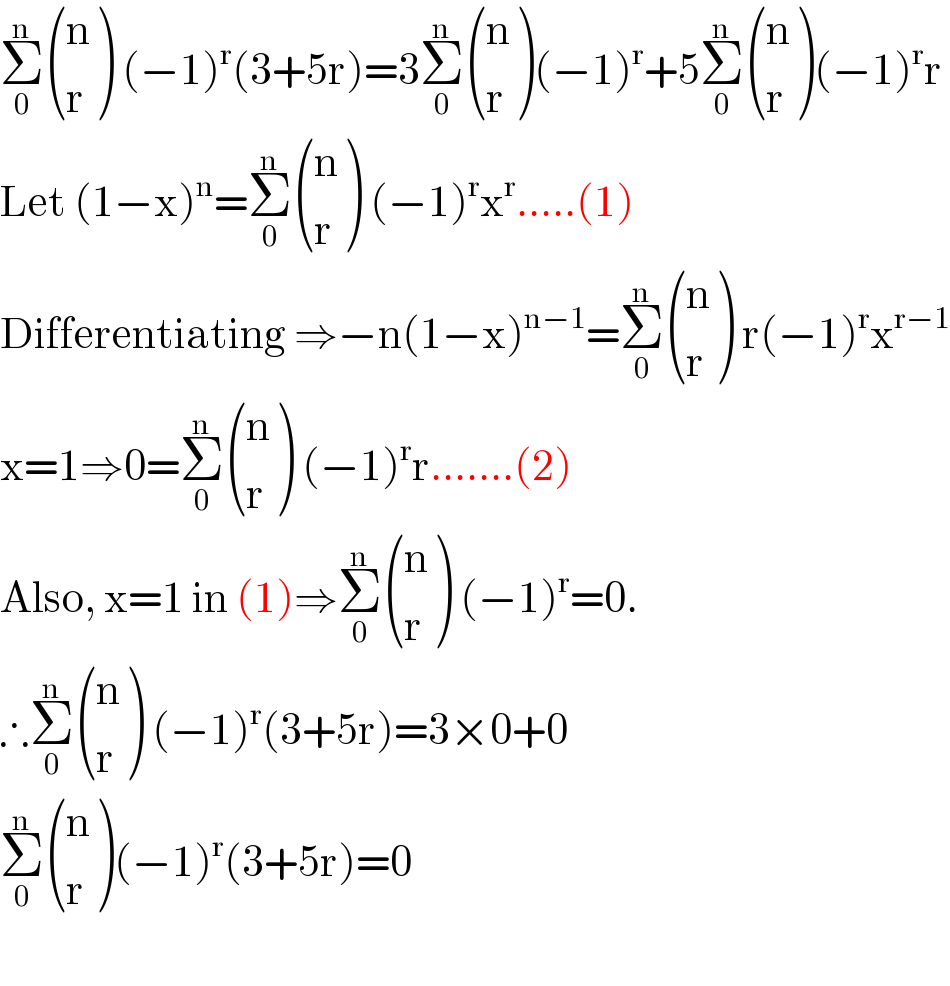
Σ_0 ^n ((n),(r) ) (−1)^r (3+5r)=3Σ_0 ^n ((n),(r) )(−1)^r +5Σ_0 ^n ((n),(r) )(−1)^r r Let (1−x)^n =Σ_0 ^n ((n),(r) ) (−1)^r x^r .....(1) Differentiating ⇒−n(1−x)^(n−1) =Σ_0 ^n ((n),(r) ) r(−1)^r x^(r−1) x=1⇒0=Σ_0 ^n ((n),(r) ) (−1)^r r.......(2) Also, x=1 in (1)⇒Σ_0 ^n ((n),(r) ) (−1)^r =0. ∴Σ_0 ^n ((n),(r) ) (−1)^r (3+5r)=3×0+0 Σ_0 ^n ((n),(r) )(−1)^r (3+5r)=0
$$\underset{\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\begin{pmatrix}{\mathrm{n}}\\{\mathrm{r}}\end{pmatrix}\:\left(−\mathrm{1}\right)^{\mathrm{r}} \left(\mathrm{3}+\mathrm{5r}\right)=\mathrm{3}\underset{\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\begin{pmatrix}{\mathrm{n}}\\{\mathrm{r}}\end{pmatrix}\left(−\mathrm{1}\right)^{\mathrm{r}} +\mathrm{5}\underset{\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\begin{pmatrix}{\mathrm{n}}\\{\mathrm{r}}\end{pmatrix}\left(−\mathrm{1}\right)^{\mathrm{r}} \mathrm{r} \\ $$$$\mathrm{Let}\:\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{n}} =\underset{\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\begin{pmatrix}{\mathrm{n}}\\{\mathrm{r}}\end{pmatrix}\:\left(−\mathrm{1}\right)^{\mathrm{r}} \mathrm{x}^{\mathrm{r}} …..\left(\mathrm{1}\right) \\ $$$$\mathrm{Differentiating}\:\Rightarrow−\mathrm{n}\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{n}−\mathrm{1}} =\underset{\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\begin{pmatrix}{\mathrm{n}}\\{\mathrm{r}}\end{pmatrix}\:\mathrm{r}\left(−\mathrm{1}\right)^{\mathrm{r}} \mathrm{x}^{\mathrm{r}−\mathrm{1}} \\ $$$$\mathrm{x}=\mathrm{1}\Rightarrow\mathrm{0}=\underset{\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\begin{pmatrix}{\mathrm{n}}\\{\mathrm{r}}\end{pmatrix}\:\left(−\mathrm{1}\right)^{\mathrm{r}} \mathrm{r}…….\left(\mathrm{2}\right) \\ $$$$\mathrm{Also},\:\mathrm{x}=\mathrm{1}\:\mathrm{in}\:\left(\mathrm{1}\right)\Rightarrow\underset{\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\begin{pmatrix}{\mathrm{n}}\\{\mathrm{r}}\end{pmatrix}\:\left(−\mathrm{1}\right)^{\mathrm{r}} =\mathrm{0}. \\ $$$$\therefore\underset{\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\begin{pmatrix}{\mathrm{n}}\\{\mathrm{r}}\end{pmatrix}\:\left(−\mathrm{1}\right)^{\mathrm{r}} \left(\mathrm{3}+\mathrm{5r}\right)=\mathrm{3}×\mathrm{0}+\mathrm{0} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\begin{pmatrix}{\mathrm{n}}\\{\mathrm{r}}\end{pmatrix}\left(−\mathrm{1}\right)^{\mathrm{r}} \left(\mathrm{3}+\mathrm{5r}\right)=\mathrm{0} \\ $$$$ \\ $$
Answered by prakash jain last updated on 02/Oct/16
answer in comments
$$\mathrm{answer}\:\mathrm{in}\:\mathrm{comments} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *