Menu Close

The-value-of-x-satisfying-the-inequalities-2x-1-x-1-4-x-2-4-x-2-x-4-4-0-

Tinku Tara 0 Comments
Pin




Question Number 72830 by Tip Top last updated on 03/Nov/19
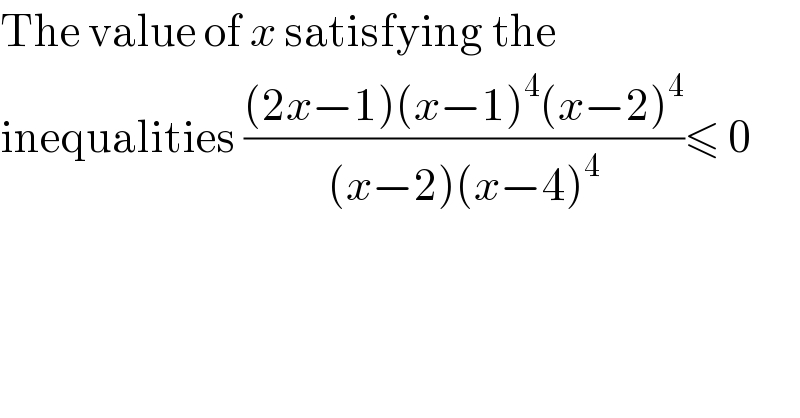
The value of x satisfying the inequalities (((2x−1)(x−1)^4 (x−2)^4 )/((x−2)(x−4)^4 ))≤ 0
$$\mathrm{The}\:\mathrm{value}\:\mathrm{of}\:{x}\:\mathrm{satisfying}\:\mathrm{the}\: \\ $$$$\mathrm{inequalities}\:\frac{\left(\mathrm{2}{x}−\mathrm{1}\right)\left({x}−\mathrm{1}\right)^{\mathrm{4}} \left({x}−\mathrm{2}\right)^{\mathrm{4}} }{\left({x}−\mathrm{2}\right)\left({x}−\mathrm{4}\right)^{\mathrm{4}} }\leqslant\:\mathrm{0} \\ $$
Answered by MJS last updated on 03/Nov/19
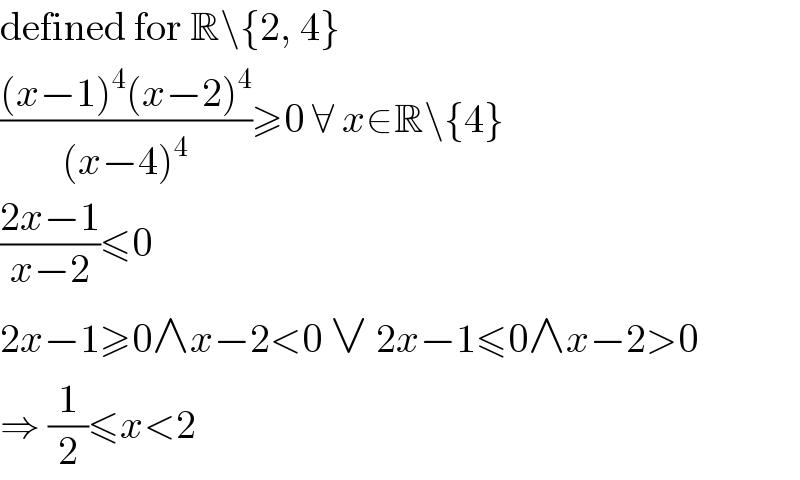
defined for R\{2, 4} (((x−1)^4 (x−2)^4 )/((x−4)^4 ))≥0 ∀ x∈R\{4} ((2x−1)/(x−2))≤0 2x−1≥0∧x−2<0 ∨ 2x−1≤0∧x−2>0 ⇒ (1/2)≤x<2
$$\mathrm{defined}\:\mathrm{for}\:\mathbb{R}\backslash\left\{\mathrm{2},\:\mathrm{4}\right\} \\ $$$$\frac{\left({x}−\mathrm{1}\right)^{\mathrm{4}} \left({x}−\mathrm{2}\right)^{\mathrm{4}} }{\left({x}−\mathrm{4}\right)^{\mathrm{4}} }\geqslant\mathrm{0}\:\forall\:{x}\in\mathbb{R}\backslash\left\{\mathrm{4}\right\} \\ $$$$\frac{\mathrm{2}{x}−\mathrm{1}}{{x}−\mathrm{2}}\leqslant\mathrm{0} \\ $$$$\mathrm{2}{x}−\mathrm{1}\geqslant\mathrm{0}\wedge{x}−\mathrm{2}<\mathrm{0}\:\vee\:\mathrm{2}{x}−\mathrm{1}\leqslant\mathrm{0}\wedge{x}−\mathrm{2}>\mathrm{0} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}}\leqslant{x}<\mathrm{2} \\ $$
Answered by Tanmay chaudhury last updated on 03/Nov/19
(x−1)^4 ,(x−2)^4 and (x−4)^4 even power so they are always +ve . x≠2 x≠ 4 critical value of x=(1/2)=0.5 and 2 f(x)=((2x−1)/((x−2)))×[(((x−1)(x−2))/((x−4)))]^4 when x>2 f(x)>0 when x<0.5 f(x)>0 when 2>x>0.5 f(x)<0 solution x∈ [0.5, 2) pls check
$$\left({x}−\mathrm{1}\right)^{\mathrm{4}} ,\left({x}−\mathrm{2}\right)^{\mathrm{4}} {and}\:\left({x}−\mathrm{4}\right)^{\mathrm{4}} \:\:{even}\:{power} \\ $$$${so}\:{they}\:{are}\:{always}\:+{ve}\:. \\ $$$${x}\neq\mathrm{2}\:\:\:\:\:{x}\neq\:\mathrm{4} \\ $$$${critical}\:{value}\:{of}\:{x}=\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0}.\mathrm{5}\:{and}\:\mathrm{2} \\ $$$${f}\left({x}\right)=\frac{\mathrm{2}{x}−\mathrm{1}}{\left({x}−\mathrm{2}\right)}×\left[\frac{\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)}{\left({x}−\mathrm{4}\right)}\right]^{\mathrm{4}} \\ $$$${when}\:{x}>\mathrm{2}\:\:{f}\left({x}\right)>\mathrm{0} \\ $$$${when}\:{x}<\mathrm{0}.\mathrm{5}\:\:{f}\left({x}\right)>\mathrm{0} \\ $$$${when}\:\:\:\:\:\mathrm{2}>{x}>\mathrm{0}.\mathrm{5}\:{f}\left({x}\right)<\mathrm{0} \\ $$$${solution}\:\:\:{x}\in\:\left[\mathrm{0}.\mathrm{5},\:\mathrm{2}\right)\:\:\boldsymbol{{pls}}\:\boldsymbol{{check}} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *