Menu Close

Three-six-faced-dice-are-thrown-together-The-probability-that-the-sum-of-the-numbers-appearing-on-the-dice-is-k-3-k-8-is-

Tinku Tara 0 Comments
Pin




Question Number 47481 by limite last updated on 10/Nov/18
Three six−faced dice are thrown together. The probability that the sum of the numbers appearing on the dice is k (3≤ k ≤ 8) is
$$\mathrm{Three}\:\mathrm{six}−\mathrm{faced}\:\mathrm{dice}\:\mathrm{are}\:\mathrm{thrown} \\ $$$$\mathrm{together}.\:\mathrm{The}\:\mathrm{probability}\:\mathrm{that}\:\mathrm{the}\:\mathrm{sum} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{numbers}\:\mathrm{appearing}\:\mathrm{on}\:\mathrm{the}\:\mathrm{dice} \\ $$$$\mathrm{is}\:\:{k}\:\left(\mathrm{3}\leqslant\:{k}\:\leqslant\:\mathrm{8}\right)\:\mathrm{is} \\ $$
Answered by ajfour last updated on 10/Nov/18
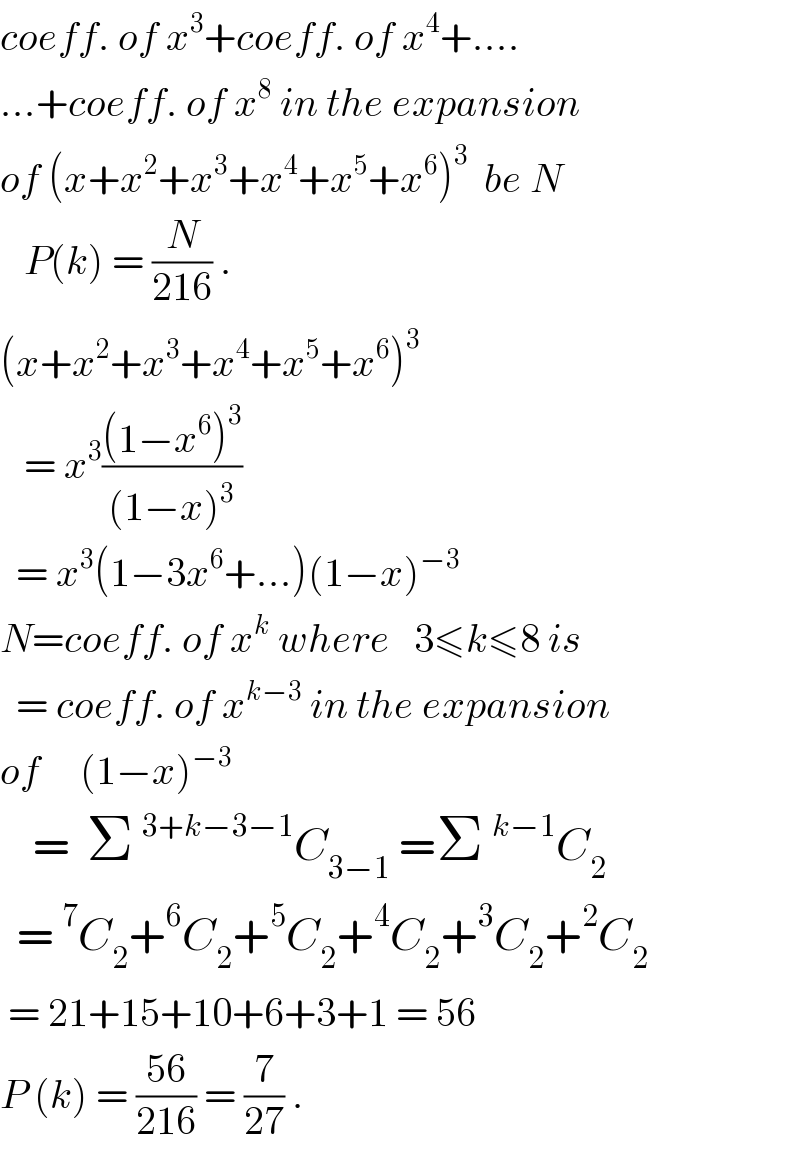
coeff. of x^3 +coeff. of x^4 +.... ...+coeff. of x^8 in the expansion of (x+x^2 +x^3 +x^4 +x^5 +x^6 )^3 be N P(k) = (N/(216)) . (x+x^2 +x^3 +x^4 +x^5 +x^6 )^3 = x^3 (((1−x^6 )^3 )/((1−x)^3 )) = x^3 (1−3x^6 +...)(1−x)^(−3) N=coeff. of x^k where 3≤k≤8 is = coeff. of x^(k−3) in the expansion of (1−x)^(−3) = Σ^(3+k−3−1) C_(3−1) =Σ^(k−1) C_2 =^7 C_2 +^6 C_2 +^5 C_2 +^4 C_2 +^3 C_2 +^2 C_2 = 21+15+10+6+3+1 = 56 P (k) = ((56)/(216)) = (7/(27)) .
$${coeff}.\:{of}\:{x}^{\mathrm{3}} +{coeff}.\:{of}\:{x}^{\mathrm{4}} +…. \\ $$$$…+{coeff}.\:{of}\:{x}^{\mathrm{8}} \:{in}\:{the}\:{expansion} \\ $$$${of}\:\left({x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +{x}^{\mathrm{4}} +{x}^{\mathrm{5}} +{x}^{\mathrm{6}} \right)^{\mathrm{3}} \:\:{be}\:{N} \\ $$$$\:\:\:{P}\left({k}\right)\:=\:\frac{{N}}{\mathrm{216}}\:. \\ $$$$\left({x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +{x}^{\mathrm{4}} +{x}^{\mathrm{5}} +{x}^{\mathrm{6}} \right)^{\mathrm{3}} \\ $$$$\:\:\:=\:{x}^{\mathrm{3}} \frac{\left(\mathrm{1}−{x}^{\mathrm{6}} \right)^{\mathrm{3}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} } \\ $$$$\:\:=\:{x}^{\mathrm{3}} \left(\mathrm{1}−\mathrm{3}{x}^{\mathrm{6}} +…\right)\left(\mathrm{1}−{x}\right)^{−\mathrm{3}} \\ $$$${N}={coeff}.\:{of}\:{x}^{{k}} \:{where}\:\:\:\mathrm{3}\leqslant{k}\leqslant\mathrm{8}\:{is} \\ $$$$\:\:=\:{coeff}.\:{of}\:{x}^{{k}−\mathrm{3}} \:{in}\:{the}\:{expansion} \\ $$$${of}\:\:\:\:\:\left(\mathrm{1}−{x}\right)^{−\mathrm{3}} \\ $$$$\:\:\:\:=\:\:\Sigma\:^{\mathrm{3}+{k}−\mathrm{3}−\mathrm{1}} {C}_{\mathrm{3}−\mathrm{1}} \:=\Sigma\:^{{k}−\mathrm{1}} {C}_{\mathrm{2}} \\ $$$$\:\:=\:^{\mathrm{7}} {C}_{\mathrm{2}} +^{\mathrm{6}} {C}_{\mathrm{2}} +^{\mathrm{5}} {C}_{\mathrm{2}} +^{\mathrm{4}} {C}_{\mathrm{2}} +^{\mathrm{3}} {C}_{\mathrm{2}} +^{\mathrm{2}} {C}_{\mathrm{2}} \\ $$$$\:=\:\mathrm{21}+\mathrm{15}+\mathrm{10}+\mathrm{6}+\mathrm{3}+\mathrm{1}\:=\:\mathrm{56} \\ $$$${P}\:\left({k}\right)\:=\:\frac{\mathrm{56}}{\mathrm{216}}\:=\:\frac{\mathrm{7}}{\mathrm{27}}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *