Question Number 193502 by horsebrand11 last updated on 15/Jun/23
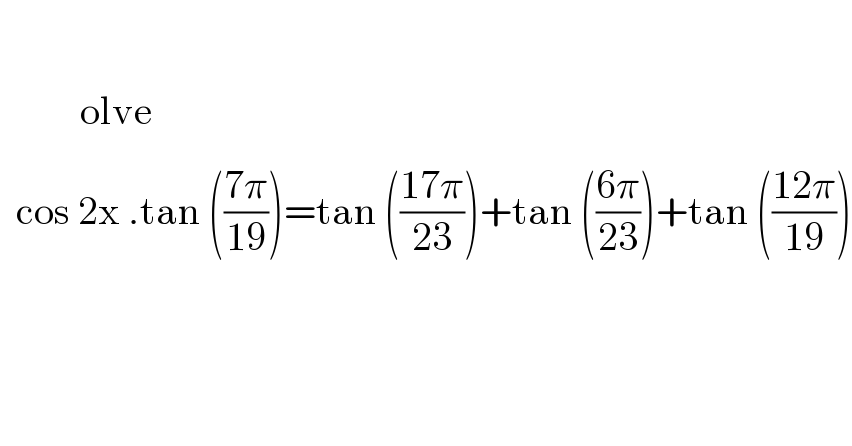
$$\:\cancel{\underline{{o}}}\mathrm{olve}\: \\ $$$$\:\:\mathrm{cos}\:\mathrm{2x}\:.\mathrm{tan}\:\left(\frac{\mathrm{7}\pi}{\mathrm{19}}\right)=\mathrm{tan}\:\left(\frac{\mathrm{17}\pi}{\mathrm{23}}\right)+\mathrm{tan}\:\left(\frac{\mathrm{6}\pi}{\mathrm{23}}\right)+\mathrm{tan}\:\left(\frac{\mathrm{12}\pi}{\mathrm{19}}\right) \\ $$
Answered by cortano12 last updated on 15/Jun/23

$$\:\:\mathrm{If}\:\alpha+\beta=\pi\:\mathrm{then}\:\begin{cases}{\mathrm{tan}\:\alpha+\mathrm{tan}\:\beta=\mathrm{0}}\\{\mathrm{tan}\:\alpha\:\mathrm{cot}\:\beta=−\mathrm{1}}\end{cases} \\ $$$$\:\mathrm{so}\:\mathrm{cos}\:\:\mathrm{2x}\:\mathrm{tan}\:\left(\frac{\mathrm{7}\pi}{\mathrm{19}}\right)=\mathrm{0}+\mathrm{tan}\:\left(\frac{\mathrm{12}\pi}{\mathrm{19}}\right) \\ $$$$\:\Leftrightarrow\:\mathrm{cos}\:\:\mathrm{2x}\:=\:−\mathrm{1}\: \\ $$$$\:\Leftrightarrow\:\mathrm{cos}\:\:\mathrm{2x}=\:\mathrm{cos}\:\pi \\ $$$$\:\Leftrightarrow\:\mathrm{x}=\pm\frac{\pi}{\mathrm{2}}\:+\mathrm{k}.\pi\: \\ $$
Commented by BaliramKumar last updated on 15/Jun/23

$$\mathrm{sin2x}\:\rightarrow\:\mathrm{cos2x} \\ $$
Answered by aba last updated on 15/Jun/23
![⇒cos2x.tg((7π)/(19))=tg(π−((6π)/(23)))+tg(((6π)/(23)))+tg(π−((7π)/(19))) ⇒cos2x.tg((7π)/(19))=−tg((6π)/(23))+tg((6π)/(23))−tg((7π)/(19)) ⇒cos2x=−1=cos(π) ⇒ { ((2x≡π[2π])),((2x≡−π[2π])) :} ⇒ { ((x≡(1/2)π[2π]=(1/2)π(2k+1))),((x≡−(1/2)π[2π]=(1/2)π(2k−1))) :}k∈Z](https://www.tinkutara.com/question/Q193508.png)
$$\Rightarrow\mathrm{cos2x}.\mathrm{tg}\frac{\mathrm{7}\pi}{\mathrm{19}}=\mathrm{tg}\left(\pi−\frac{\mathrm{6}\pi}{\mathrm{23}}\right)+\mathrm{tg}\left(\frac{\mathrm{6}\pi}{\mathrm{23}}\right)+\mathrm{tg}\left(\pi−\frac{\mathrm{7}\pi}{\mathrm{19}}\right) \\ $$$$\Rightarrow\mathrm{cos2x}.\mathrm{tg}\frac{\mathrm{7}\pi}{\mathrm{19}}=−\mathrm{tg}\frac{\mathrm{6}\pi}{\mathrm{23}}+\mathrm{tg}\frac{\mathrm{6}\pi}{\mathrm{23}}−\mathrm{tg}\frac{\mathrm{7}\pi}{\mathrm{19}} \\ $$$$\Rightarrow\mathrm{cos2x}=−\mathrm{1}=\mathrm{cos}\left(\pi\right) \\ $$$$\Rightarrow\begin{cases}{\mathrm{2x}\equiv\pi\left[\mathrm{2}\pi\right]}\\{\mathrm{2x}\equiv−\pi\left[\mathrm{2}\pi\right]}\end{cases}\:\Rightarrow\begin{cases}{\mathrm{x}\equiv\frac{\mathrm{1}}{\mathrm{2}}\pi\left[\mathrm{2}\pi\right]=\frac{\mathrm{1}}{\mathrm{2}}\pi\left(\mathrm{2k}+\mathrm{1}\right)}\\{\mathrm{x}\equiv−\frac{\mathrm{1}}{\mathrm{2}}\pi\left[\mathrm{2}\pi\right]=\frac{\mathrm{1}}{\mathrm{2}}\pi\left(\mathrm{2k}−\mathrm{1}\right)}\end{cases}\mathrm{k}\in\mathbb{Z} \\ $$
