Question-193754

Question Number 193754 by Mingma last updated on 19/Jun/23

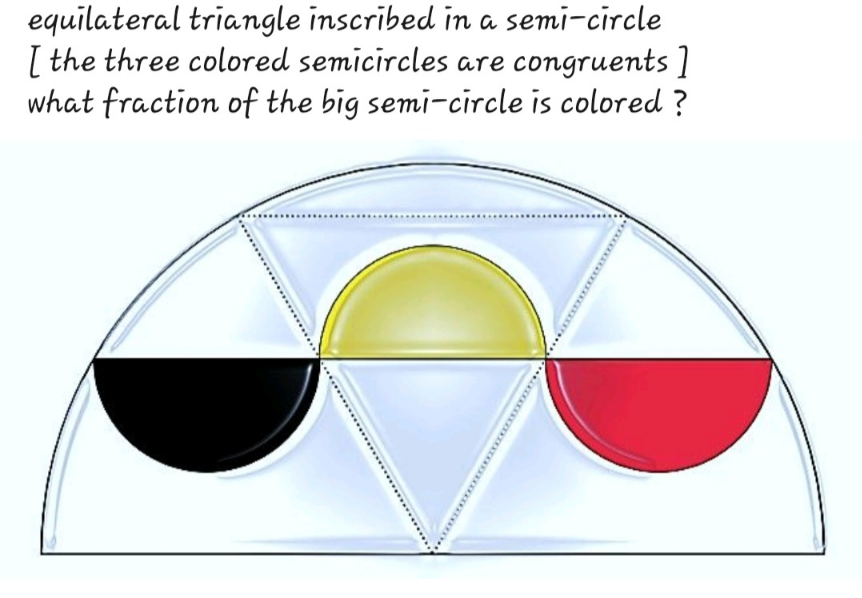
Answered by talminator2856792 last updated on 19/Jun/23

let R, r represent radius of big semicircle and small semicricle, respectively. by pythagorean theorem: R = (√((((r(√3))/2))^2 + (3r)^2 )) R = (√(((3r^2 )/4) + 9r^2 )) R = (√((39r^2 )/4)) R = ((r(√(39)))/2) fraction of big semicircle shaded = 3 × (( ((πr^2 )/2) )/( ((πR^2 )/2) )) = 3 × (r^2 /R^2 ) = 3 × (r^2 /( ((39r^2 )/4) )) = 3 × (1/( ((39)/4) )) = ((12)/(39))

$$\:\:\mathrm{let}\:{R},\:{r}\:\:\mathrm{represent}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{big}\:\mathrm{semicircle}\:\:\: \\ $$$$\:\:\mathrm{and}\:\mathrm{small}\:\mathrm{semicricle},\:\mathrm{respectively}. \\ $$$$\:\:\mathrm{by}\:\mathrm{pythagorean}\:\mathrm{theorem}: \\ $$$$\:\:{R}\:=\:\sqrt{\left(\frac{{r}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\:\left(\mathrm{3}{r}\right)^{\mathrm{2}} \:} \\ $$$$\:\:{R}\:=\:\sqrt{\frac{\mathrm{3}{r}^{\mathrm{2}} }{\mathrm{4}}\:+\:\mathrm{9}{r}^{\mathrm{2}} \:} \\ $$$$\:\:{R}\:=\:\sqrt{\frac{\mathrm{39}{r}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$$\:\:{R}\:=\:\frac{{r}\sqrt{\mathrm{39}}}{\mathrm{2}} \\ $$$$\:\:\mathrm{fraction}\:\mathrm{of}\:\mathrm{big}\:\mathrm{semicircle}\:\mathrm{shaded}\:\: \\ $$$$\:\:=\:\mathrm{3}\:×\:\frac{\:\frac{\pi{r}^{\mathrm{2}} }{\mathrm{2}}\:}{\:\frac{\pi{R}^{\mathrm{2}} }{\mathrm{2}}\:}\: \\ $$$$\:\:=\:\mathrm{3}\:×\:\frac{{r}^{\mathrm{2}} }{{R}^{\mathrm{2}} }\: \\ $$$$\:\:=\:\mathrm{3}\:×\:\frac{{r}^{\mathrm{2}} }{\:\frac{\mathrm{39}{r}^{\mathrm{2}} }{\mathrm{4}}\:}\: \\ $$$$\:\:=\:\mathrm{3}\:×\:\frac{\mathrm{1}}{\:\frac{\mathrm{39}}{\mathrm{4}}\:} \\ $$$$\:\:=\:\frac{\mathrm{12}}{\mathrm{39}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply