Question Number 193880 by Mingma last updated on 22/Jun/23
Answered by Subhi last updated on 22/Jun/23
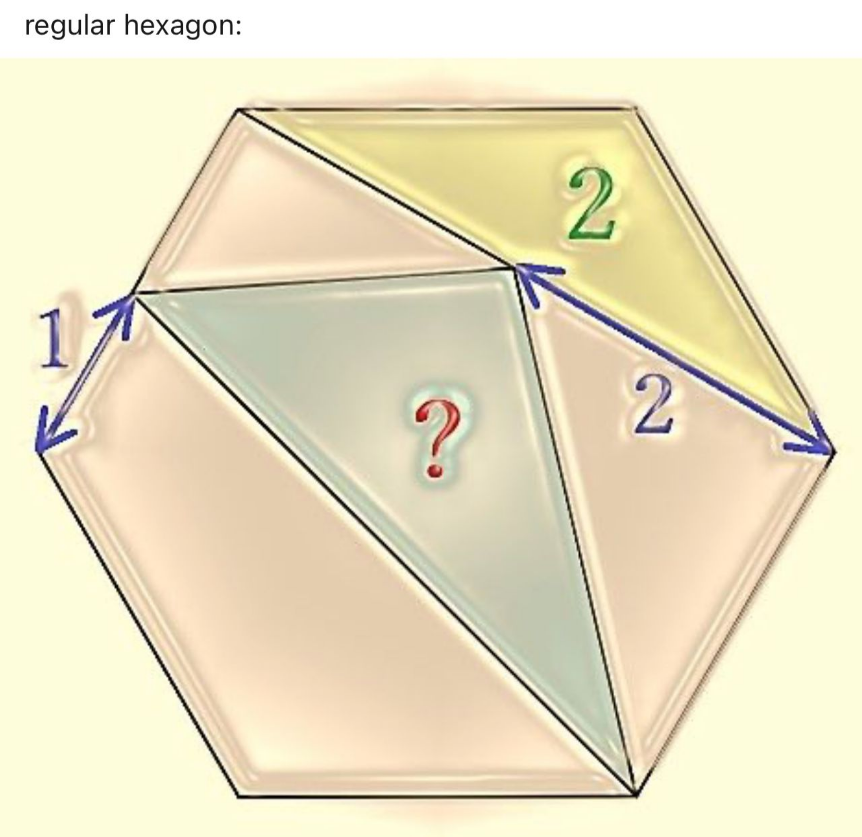
![put length of each side = l BAF = 120 ⇛ AFB = ABF = ((180−120)/2)=30 ((BF)/(sin(120)))=(l/(sin(30))) ⇛ BF = (√3) l (1/2)l^2 . sin(120)=2 ⇛ l = (√((8(√3))/3)) BF = 3.7224 ⇛ BG = 1.7224 EG = (√(((8(√3))/3)+2^2 ))=2.936 IG = (√(((√((8(√3))/3))−1)^2 +(1.7224)^2 ))= 2.07 IGH = 180−(tan^(−1) ((l/2))+tan^(−1) (((l−1)/( (√3)l−2))))=99.23 [IGH] = (1/2)×sin(99.23)×2.07×2.936 = 3](https://www.tinkutara.com/question/Q193881.png)
$${put}\:{length}\:{of}\:{each}\:{side}\:=\:{l} \\ $$$${BAF}\:=\:\mathrm{120}\:\Rrightarrow\:{AFB}\:=\:{ABF}\:=\:\frac{\mathrm{180}−\mathrm{120}}{\mathrm{2}}=\mathrm{30} \\ $$$$\frac{{BF}}{{sin}\left(\mathrm{120}\right)}=\frac{{l}}{{sin}\left(\mathrm{30}\right)}\:\Rrightarrow\:{BF}\:=\:\sqrt{\mathrm{3}}\:{l}\: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{l}^{\mathrm{2}} \:.\:{sin}\left(\mathrm{120}\right)=\mathrm{2}\:\:\Rrightarrow\:{l}\:=\:\sqrt{\frac{\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{3}}} \\ $$$${BF}\:=\:\mathrm{3}.\mathrm{7224}\:\:\Rrightarrow\:{BG}\:=\:\mathrm{1}.\mathrm{7224} \\ $$$${EG}\:=\:\sqrt{\frac{\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{3}}+\mathrm{2}^{\mathrm{2}} }=\mathrm{2}.\mathrm{936} \\ $$$${IG}\:=\:\sqrt{\left(\sqrt{\frac{\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{3}}}−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{1}.\mathrm{7224}\right)^{\mathrm{2}} }=\:\mathrm{2}.\mathrm{07} \\ $$$${IGH}\:=\:\mathrm{180}−\left({tan}^{−\mathrm{1}} \left(\frac{{l}}{\mathrm{2}}\right)+{tan}^{−\mathrm{1}} \left(\frac{{l}−\mathrm{1}}{\:\sqrt{\mathrm{3}}{l}−\mathrm{2}}\right)\right)=\mathrm{99}.\mathrm{23} \\ $$$$\left[{IGH}\right]\:=\:\frac{\mathrm{1}}{\mathrm{2}}×{sin}\left(\mathrm{99}.\mathrm{23}\right)×\mathrm{2}.\mathrm{07}×\mathrm{2}.\mathrm{936}\:=\:\mathrm{3} \\ $$
Commented by Subhi last updated on 22/Jun/23

Commented by Mingma last updated on 22/Jun/23
Perfect ��
