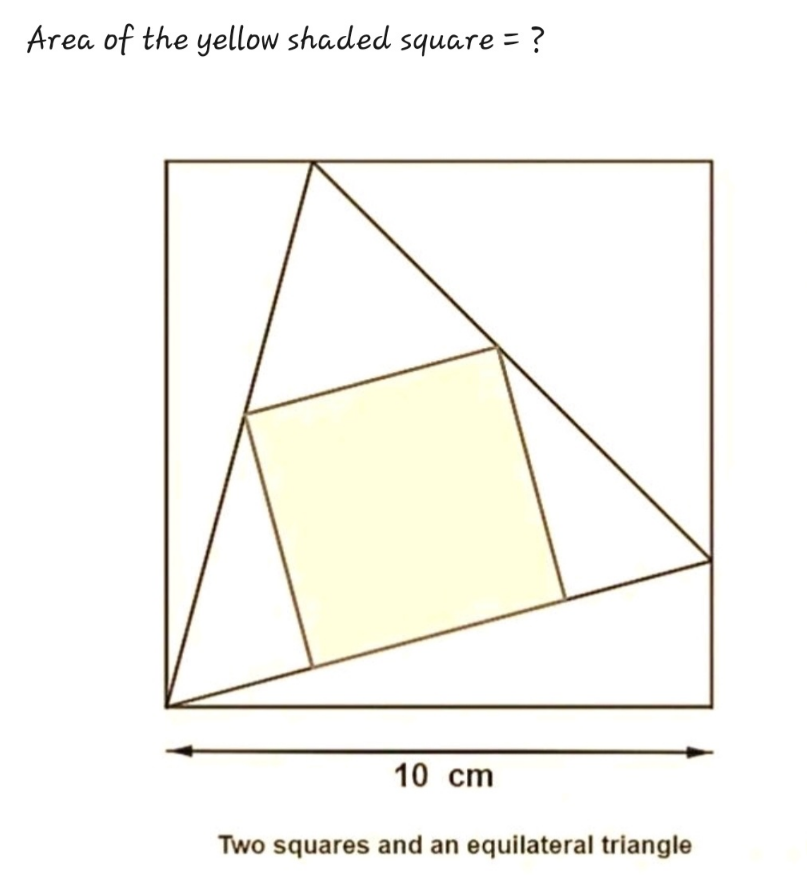
Question Number 194067 by Rupesh123 last updated on 27/Jun/23
Answered by som(math1967) last updated on 27/Jun/23

$$\:{x}^{\mathrm{2}} +\mathrm{10}^{\mathrm{2}} =\mathrm{2}\left(\mathrm{10}−{x}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −\mathrm{40}{x}+\mathrm{100}=\mathrm{0} \\ $$$$\:{x}=\mathrm{10}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right) \\ $$$${side}\:{of}\:{triangle}=\sqrt{\mathrm{2}}×\mathrm{10}\left(\mathrm{1}−\mathrm{2}+\sqrt{\mathrm{3}}\right) \\ $$$$=\mathrm{10}\sqrt{\mathrm{2}}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right) \\ $$$$\:\frac{{a}}{\mathrm{10}\sqrt{\mathrm{2}}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)−{a}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\: \\ $$$$\mathrm{2}{a}=\mathrm{30}\sqrt{\mathrm{2}}−\mathrm{10}\sqrt{\mathrm{6}}−\sqrt{\mathrm{3}}{a} \\ $$$$\:\therefore{a}=\frac{\mathrm{10}\left(\mathrm{3}\sqrt{\mathrm{2}}−\sqrt{\mathrm{6}}\right)}{\mathrm{2}+\sqrt{\mathrm{3}}} \\ $$$$\:{a}^{\mathrm{2}} =\frac{\mathrm{100}\left(\mathrm{3}\sqrt{\mathrm{2}}−\sqrt{\mathrm{6}}\right)^{\mathrm{2}} }{\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }{cm}^{\mathrm{2}} \\ $$
Commented by som(math1967) last updated on 27/Jun/23

Commented by Frix last updated on 27/Jun/23

$$\mathrm{I}'\mathrm{m}\:\mathrm{afraid}\:\mathrm{there}'\mathrm{s}\:\mathrm{a}\:\mathrm{mistake}\:\mathrm{calculating}\:{a}. \\ $$$$\mathrm{I}\:\mathrm{get}\:{a}=\mathrm{10}\left(\mathrm{9}−\mathrm{5}\sqrt{\mathrm{3}}\right)\sqrt{\mathrm{2}}\approx\mathrm{4}.\mathrm{80} \\ $$$$\mathrm{while}\:\mathrm{your}\:{a}\approx\mathrm{1}.\mathrm{24} \\ $$$$\mathrm{which}\:\mathrm{seems}\:\mathrm{too}\:\mathrm{small}\:\mathrm{given}\:\mathrm{the}\:\mathrm{side}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{triangle}\:\mathrm{is}\:\approx\mathrm{10}.\mathrm{35} \\ $$
Commented by som(math1967) last updated on 27/Jun/23

$${Thank}\:{you}\:{sir}\:,{I}\:{correct}\:{it} \\ $$
Commented by Rupesh123 last updated on 27/Jun/23
Perfect ��
Commented by Rupesh123 last updated on 27/Jun/23
You're right!
Answered by mr W last updated on 27/Jun/23

$${s}={side}\:{length}\:{of}\:{equilateral} \\ $$$${s}^{\mathrm{2}} =\mathrm{10}^{\mathrm{2}} +\left(\mathrm{10}−\frac{{s}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} \\ $$$$−\mathrm{400}+\mathrm{20}\sqrt{\mathrm{2}}{s}+{s}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{s}=\mathrm{10}\left(\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}\right) \\ $$$${a}={side}\:{length}\:{of}\:{small}\:{square} \\ $$$${a}+\frac{\mathrm{2}{a}}{\:\sqrt{\mathrm{3}}}={s} \\ $$$$\Rightarrow{a}=\frac{\sqrt{\mathrm{3}}{s}}{\:\sqrt{\mathrm{3}}+\mathrm{2}}=\frac{\mathrm{10}\left(\mathrm{3}\sqrt{\mathrm{2}}−\sqrt{\mathrm{6}}\right)}{\:\sqrt{\mathrm{3}}+\mathrm{2}}\approx\mathrm{4}.\mathrm{805} \\ $$
Commented by Rupesh123 last updated on 27/Jun/23
Perfect ��
