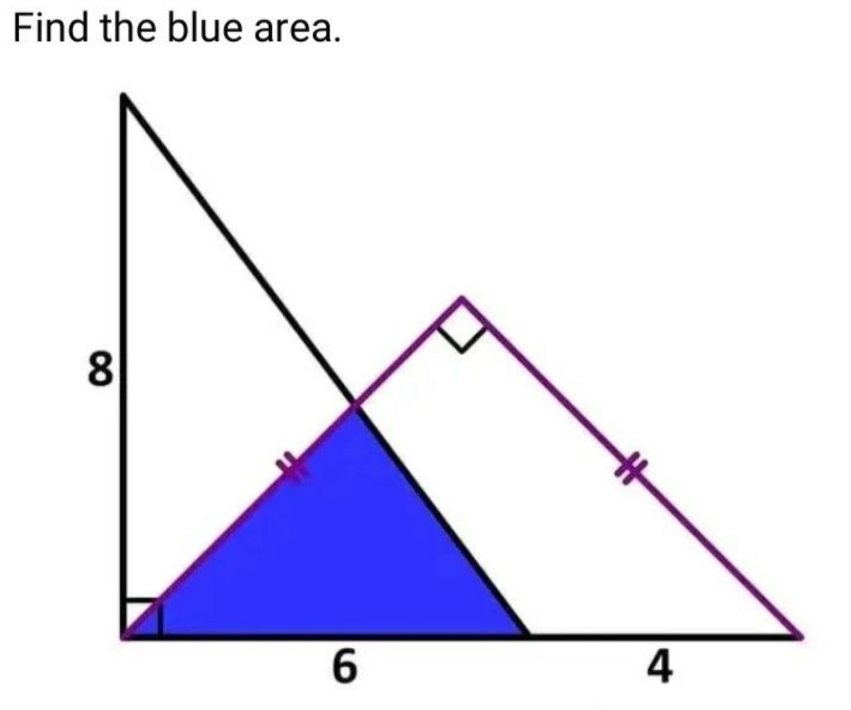
Question Number 194127 by Rupesh123 last updated on 28/Jun/23
Answered by MM42 last updated on 28/Jun/23

$${AC}={CE}\Rightarrow<{CAE}=\mathrm{45}\Rightarrow{BH}={AH} \\ $$$$\frac{{BH}}{\mathrm{8}}=\frac{{HF}}{\mathrm{6}}\Rightarrow\mathrm{3}{BH}=\mathrm{4}\left(\mathrm{6}−{BH}\right) \\ $$$$\Rightarrow{BH}=\frac{\mathrm{24}}{\mathrm{7}}\Rightarrow{S}=\frac{\mathrm{72}}{\mathrm{7}}\: \\ $$$$ \\ $$
Answered by cortano12 last updated on 28/Jun/23

$$\:\:\:\Rightarrow\mathrm{t}+\frac{\mathrm{3}}{\mathrm{4}}\mathrm{t}\:=\:\mathrm{6}\:;\:\mathrm{t}=\begin{array}{|c|}{\frac{\mathrm{24}}{\mathrm{7}}}\\\hline\end{array} \\ $$$$\:\:\Rightarrow\mathrm{blue}\:\mathrm{area}\:=\:\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{6}×\frac{\mathrm{24}}{\mathrm{7}}\:=\:\begin{array}{|c|}{\frac{\mathrm{72}}{\mathrm{7}}}\\\hline\end{array} \\ $$
