Menu Close

Question-194466

Tinku Tara 0 Comments
Pin




Question Number 194466 by horsebrand11 last updated on 08/Jul/23
⋐
$$\:\:\:\:\Subset \\ $$
Answered by cortano12 last updated on 08/Jul/23
⋐
$$\:\:\:\underbrace{\Subset} \\ $$
Answered by witcher3 last updated on 08/Jul/23
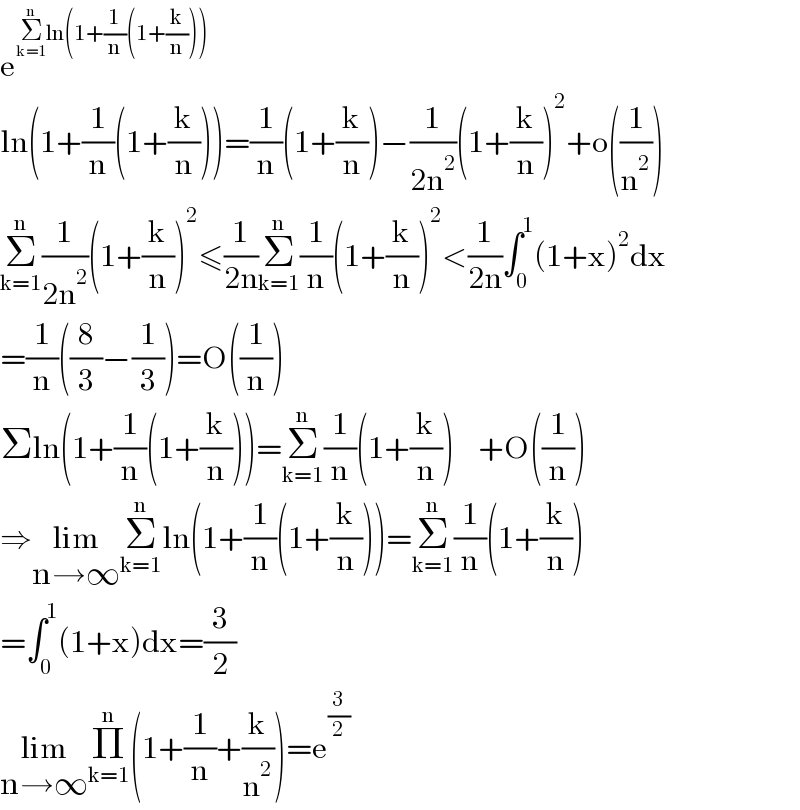
e^(Σ_(k=1) ^n ln(1+(1/n)(1+(k/n)))) ln(1+(1/n)(1+(k/n)))=(1/n)(1+(k/n))−(1/(2n^2 ))(1+(k/n))^2 +o((1/n^2 )) Σ_(k=1) ^n (1/(2n^2 ))(1+(k/n))^2 ≤(1/(2n))Σ_(k=1) ^n (1/n)(1+(k/n))^2 <(1/(2n))∫_0 ^1 (1+x)^2 dx =(1/n)((8/3)−(1/3))=O((1/n)) Σln(1+(1/n)(1+(k/n)))=Σ_(k=1) ^n (1/n)(1+(k/n)) +O((1/n)) ⇒lim_(n→∞) Σ_(k=1) ^n ln(1+(1/n)(1+(k/n)))=Σ_(k=1) ^n (1/n)(1+(k/n)) =∫_0 ^1 (1+x)dx=(3/2) lim_(n→∞) Π_(k=1) ^n (1+(1/n)+(k/n^2 ))=e^(3/2)
$$\mathrm{e}^{\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)\right)} \\ $$$$\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)\right)=\frac{\mathrm{1}}{\mathrm{n}}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)−\frac{\mathrm{1}}{\mathrm{2n}^{\mathrm{2}} }\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)^{\mathrm{2}} +\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\right) \\ $$$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{2n}^{\mathrm{2}} }\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)^{\mathrm{2}} \leqslant\frac{\mathrm{1}}{\mathrm{2n}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{n}}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)^{\mathrm{2}} <\frac{\mathrm{1}}{\mathrm{2n}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{2}} \mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{n}}\left(\frac{\mathrm{8}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}\right)=\mathrm{O}\left(\frac{\mathrm{1}}{\mathrm{n}}\right) \\ $$$$\Sigma\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)\right)=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{n}}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)\:\:\:\:+\mathrm{O}\left(\frac{\mathrm{1}}{\mathrm{n}}\right) \\ $$$$\Rightarrow\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)\right)=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{n}}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+\mathrm{x}\right)\mathrm{dx}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\prod}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}+\frac{\mathrm{k}}{\mathrm{n}^{\mathrm{2}} }\right)=\mathrm{e}^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *