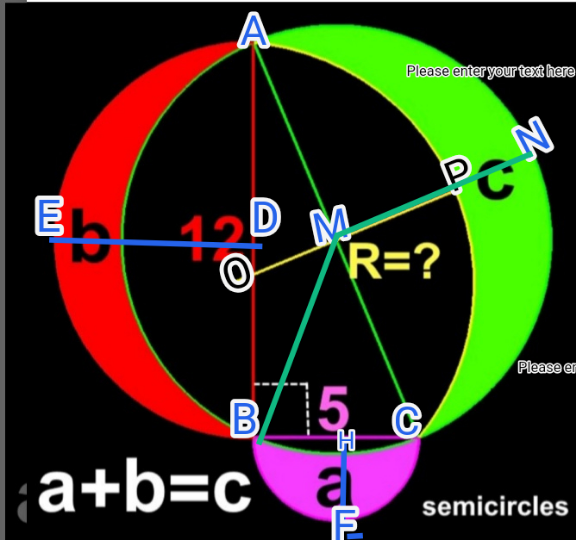
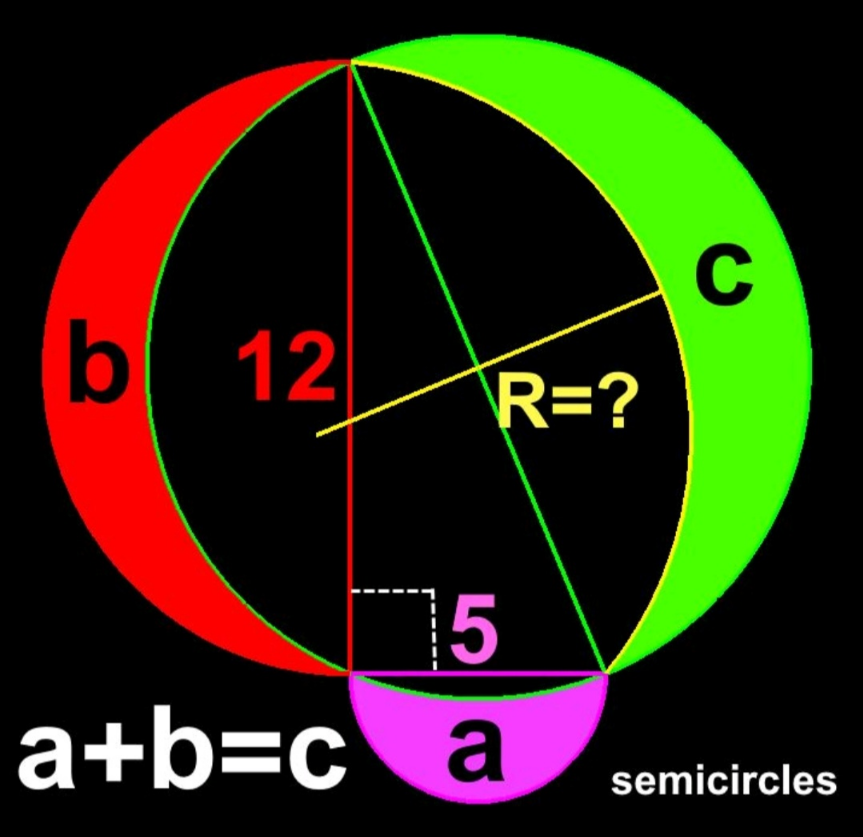
Question Number 194967 by Rupesh123 last updated on 21/Jul/23
Answered by a.lgnaoui last updated on 23/Jul/23
![4 cercles disposes comme suit •1) cercle Rouge C1(Rayon R1) 2R1=AB=12 R1=6 •2) cercle Vert C2(Rayon R2) / demi−cercle C(A,B,C) 2R2=AC=(√(12^2 −5^2 )) =13 R2=6,5 •3)cercle Noir: C(Rayon R a determiner) Espace entre C1 et C2 (Aire=b) Espace entre C2 et C (Aire=c) •3)Portion de cercle C2 delimite par arc (BC) diametre BC=5 (R3=2,5) Calcul de; a ;b; c ∗ Calcul de (a) Aire (arc MBC forme par angle 𝛉) (sin (θ/2)=((BC/2)/(AM))=((2,5)/(6,5))=(5/(13))) θ=45,25 Aire( arcMBC)=a_1 =((π×(6,5)^2 ×45,25)/(360)) a_1 =5,3𝛑 portion(BHC)=a_1 −(aire triangle MBC) a_1 −((BC)/2)×MCcos (θ/2)=2,5×6,5×0,923=15 portion BHC=5,3𝛑−15 ⇒a=𝛑×(2,5)^2 /2+15−5,3𝛑 Aire a=15−2,175𝛑 ∗calcul de l aire( b) b=𝛑×[(6,5)^2 −6^2 ]=6,25𝛑 ∗Calcul de c c=𝛑R^2 −𝛑×(6,5)^2 =𝛑(R^2 −42,25) Aire c=𝛑R^2 −42,25𝛑 c=a+b ⇒ 𝛑R^2 −42,25𝛑=15−2,175𝛑+6,25𝛑 𝛑R^2 −(42,25+6,25−2,175)𝛑=15 𝛑R^2 −46,32𝛑=15 ⇒ R^2 =46,25+((15)/𝛑) le Rayon : R=(√(46,25+((15)/𝛑)))](https://www.tinkutara.com/question/Q195076.png)
$$\mathrm{4}\:\mathrm{cercles}\:\mathrm{disposes}\:\mathrm{comme}\:\mathrm{suit} \\ $$$$\left.\bullet\mathrm{1}\right)\:\:\mathrm{cercle}\:\boldsymbol{\mathrm{R}}\mathrm{ouge}\:\boldsymbol{\mathrm{C}}\mathrm{1}\left(\mathrm{Rayon}\:\boldsymbol{\mathrm{R}}\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\mathrm{2}\boldsymbol{\mathrm{R}}\mathrm{1}=\boldsymbol{\mathrm{AB}}=\mathrm{12}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{R}}\mathrm{1}=\mathrm{6} \\ $$$$\left.\bullet\mathrm{2}\right)\:\mathrm{cercle}\:\boldsymbol{\mathrm{V}}\mathrm{ert}\:\boldsymbol{\mathrm{C}}\mathrm{2}\left(\boldsymbol{\mathrm{R}}\mathrm{ayon}\:\boldsymbol{\mathrm{R}}\mathrm{2}\right)\:/ \\ $$$$\:\:\:\:\:\mathrm{demi}−\mathrm{cercle}\:\:\boldsymbol{\mathrm{C}}\left(\boldsymbol{\mathrm{A}},\boldsymbol{\mathrm{B}},\boldsymbol{\mathrm{C}}\right) \\ $$$$\:\:\:\:\mathrm{2}\boldsymbol{\mathrm{R}}\mathrm{2}=\boldsymbol{\mathrm{AC}}=\sqrt{\mathrm{12}^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} \:}\:=\mathrm{13}\:\:\boldsymbol{\mathrm{R}}\mathrm{2}=\mathrm{6},\mathrm{5}\: \\ $$$$\left.\bullet\mathrm{3}\right)\mathrm{cercle}\:\boldsymbol{\mathrm{Noir}}:\:\boldsymbol{\mathrm{C}}\left(\boldsymbol{\mathrm{Rayon}}\:\boldsymbol{\mathrm{R}}\:\mathrm{a}\:\mathrm{determiner}\right) \\ $$$$ \\ $$$$\:\:\boldsymbol{\mathrm{Espace}}\:\boldsymbol{\mathrm{entre}}\:\boldsymbol{\mathrm{C}}\mathrm{1}\:\boldsymbol{\mathrm{et}}\:\boldsymbol{\mathrm{C}}\mathrm{2}\:\left(\boldsymbol{\mathrm{Aire}}=\boldsymbol{\mathrm{b}}\right) \\ $$$$\:\:\boldsymbol{\mathrm{Espace}}\:\boldsymbol{\mathrm{entre}}\:\boldsymbol{\mathrm{C}}\mathrm{2}\:\boldsymbol{\mathrm{et}}\:\boldsymbol{\mathrm{C}}\:\:\:\left(\boldsymbol{\mathrm{Aire}}=\boldsymbol{\mathrm{c}}\right) \\ $$$$\left.\:\:\bullet\mathrm{3}\right)\boldsymbol{\mathrm{Portion}}\:\boldsymbol{\mathrm{de}}\:\boldsymbol{\mathrm{cercle}}\:\boldsymbol{\mathrm{C}}\mathrm{2}\:\boldsymbol{\mathrm{delimite}}\:\boldsymbol{\mathrm{par}}\: \\ $$$$\:\:\mathrm{arc}\:\left(\mathrm{BC}\right)\:\boldsymbol{\mathrm{diametre}}\:\boldsymbol{\mathrm{BC}}=\mathrm{5}\:\:\:\left(\boldsymbol{\mathrm{R}}\mathrm{3}=\mathrm{2},\mathrm{5}\right) \\ $$$$\:\:\: \\ $$$$\boldsymbol{\mathrm{Calcul}}\:\boldsymbol{\mathrm{de}};\:\boldsymbol{\mathrm{a}}\:;\boldsymbol{\mathrm{b}};\:\boldsymbol{\mathrm{c}} \\ $$$$\:\ast\:\mathrm{Calcul}\:\mathrm{de}\:\left(\mathrm{a}\right) \\ $$$$\:\:\mathrm{Aire}\:\left(\mathrm{arc}\:\boldsymbol{\mathrm{MBC}}\:\mathrm{forme}\:\mathrm{par}\:\mathrm{angle}\:\boldsymbol{\theta}\right) \\ $$$$\:\:\left(\mathrm{sin}\:\frac{\theta}{\mathrm{2}}=\frac{\mathrm{BC}/\mathrm{2}}{\mathrm{AM}}=\frac{\mathrm{2},\mathrm{5}}{\mathrm{6},\mathrm{5}}=\frac{\mathrm{5}}{\mathrm{13}}\right)\:\theta=\mathrm{45},\mathrm{25} \\ $$$$\mathrm{Aire}\left(\:\mathrm{arcMBC}\right)=\mathrm{a}_{\mathrm{1}} =\frac{\pi×\left(\mathrm{6},\mathrm{5}\right)^{\mathrm{2}} ×\mathrm{45},\mathrm{25}}{\mathrm{360}} \\ $$$$\:\:\mathrm{a}_{\mathrm{1}} \:\:\:=\mathrm{5},\mathrm{3}\boldsymbol{\pi} \\ $$$$\mathrm{portion}\left(\mathrm{BHC}\right)=\mathrm{a}_{\mathrm{1}} −\left(\mathrm{aire}\:\mathrm{triangle}\:\mathrm{MBC}\right) \\ $$$$\mathrm{a}_{\mathrm{1}} −\frac{\mathrm{BC}}{\mathrm{2}}×\mathrm{MCcos}\:\frac{\theta}{\mathrm{2}}=\mathrm{2},\mathrm{5}×\mathrm{6},\mathrm{5}×\mathrm{0},\mathrm{923}=\mathrm{15} \\ $$$$\mathrm{portion}\:\mathrm{BHC}=\mathrm{5},\mathrm{3}\boldsymbol{\pi}−\mathrm{15} \\ $$$$\Rightarrow\boldsymbol{\mathrm{a}}=\boldsymbol{\pi}×\left(\mathrm{2},\mathrm{5}\right)^{\mathrm{2}} /\mathrm{2}+\mathrm{15}−\mathrm{5},\mathrm{3}\boldsymbol{\pi} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{Aire}\:\:\boldsymbol{\mathrm{a}}=\mathrm{15}−\mathrm{2},\mathrm{175}\boldsymbol{\pi} \\ $$$$ \\ $$$$\ast\mathrm{calcul}\:\mathrm{de}\:\mathrm{l}\:\mathrm{aire}\left(\:\boldsymbol{\mathrm{b}}\right) \\ $$$$\boldsymbol{\mathrm{b}}=\boldsymbol{\pi}×\left[\left(\mathrm{6},\mathrm{5}\right)^{\mathrm{2}} −\mathrm{6}^{\mathrm{2}} \right]=\mathrm{6},\mathrm{25}\boldsymbol{\pi} \\ $$$$\ast\mathrm{Calcul}\:\mathrm{de}\:\boldsymbol{\mathrm{c}} \\ $$$$\:\:\boldsymbol{\mathrm{c}}=\boldsymbol{\pi\mathrm{R}}^{\mathrm{2}} −\boldsymbol{\pi}×\left(\mathrm{6},\mathrm{5}\right)^{\mathrm{2}} =\boldsymbol{\pi}\left(\boldsymbol{\mathrm{R}}^{\mathrm{2}} −\mathrm{42},\mathrm{25}\right) \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{Aire}\:\:\:\boldsymbol{\mathrm{c}}=\boldsymbol{\pi\mathrm{R}}^{\mathrm{2}} −\mathrm{42},\mathrm{25}\boldsymbol{\pi} \\ $$$$ \\ $$$$\boldsymbol{\mathrm{c}}=\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{b}}\:\:\Rightarrow \\ $$$$\:\boldsymbol{\pi}\mathrm{R}^{\mathrm{2}} −\mathrm{42},\mathrm{25}\boldsymbol{\pi}=\mathrm{15}−\mathrm{2},\mathrm{175}\boldsymbol{\pi}+\mathrm{6},\mathrm{25}\boldsymbol{\pi} \\ $$$$\boldsymbol{\pi\mathrm{R}}^{\mathrm{2}} −\left(\mathrm{42},\mathrm{25}+\mathrm{6},\mathrm{25}−\mathrm{2},\mathrm{175}\right)\boldsymbol{\pi}=\mathrm{15} \\ $$$$\boldsymbol{\pi\mathrm{R}}^{\mathrm{2}} −\mathrm{46},\mathrm{32}\boldsymbol{\pi}=\mathrm{15}\: \\ $$$$\:\:\Rightarrow\:\:\:\:\boldsymbol{\mathrm{R}}^{\mathrm{2}} =\mathrm{46},\mathrm{25}+\frac{\mathrm{15}}{\boldsymbol{\pi}} \\ $$$$\:\: \\ $$$$\:\:\:\:\:\:\mathrm{le}\:\mathrm{Rayon}\::\:\:\boldsymbol{\mathrm{R}}=\sqrt{\mathrm{46},\mathrm{25}+\frac{\mathrm{15}}{\boldsymbol{\pi}}} \\ $$$$ \\ $$$$\: \\ $$
Commented by a.lgnaoui last updated on 23/Jul/23