Question Number 195229 by mathlove last updated on 28/Jul/23

$${below}\:{equestion}\:{is}\:{show}\:\:{elips}\:{and} \\ $$$${hypharabollah} \\ $$$$\frac{{x}^{\mathrm{2}} }{{cos}\mathrm{3}}+\frac{{y}^{\mathrm{2}} }{{sin}\mathrm{3}}=\mathrm{1} \\ $$
Commented by mr W last updated on 28/Jul/23

$$\frac{\pi}{\mathrm{2}}<\mathrm{3}<\pi \\ $$$$\Rightarrow\mathrm{cos}\:\mathrm{3}\:<\mathrm{0} \\ $$
Commented by AST last updated on 28/Jul/23

$${Yea},{if}\:\mathrm{3}\:{is}\:{in}\:{radians}.\:{But}\:\sqrt{{cos}\:\mathrm{3}}\:{would}\:{not}\:{be}\: \\ $$$${real}.\:{If}\:\mathrm{3}\:{is}\:{in}\:{degrees},\:{then}\:{cos}\mathrm{3}>\mathrm{0}. \\ $$
Commented by AST last updated on 28/Jul/23

$$“{hypharabollah}''?\: \\ $$
Commented by mathlove last updated on 28/Jul/23

$${way} \\ $$$${cos}\mathrm{3}\overset{?} {<}\mathrm{0} \\ $$
Commented by AST last updated on 28/Jul/23

$$\frac{{x}^{\mathrm{2}} }{\:\left(\sqrt{{cos}\mathrm{3}}\right)^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{\left(\sqrt{{sin}\mathrm{3}}\right)^{\mathrm{2}} }=\mathrm{1}\:\left({since}\:{cos}\mathrm{3},{sin}\mathrm{3}>\mathrm{0}\right) \\ $$$${Has}\:{the}\:{form}\:{of}\:{an}\:{ellipse}:\:\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$
Commented by AST last updated on 28/Jul/23

$$“{Hyperbola}''\:{is}\:{of}\:{the}\:{form}\:\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$
Commented by mathlove last updated on 28/Jul/23

$${i}\:{understand}\:\mathrm{3}\:{is}\:{no}\:{degree} \\ $$$${but}\:\mathrm{3}\:{is}\:{radian} \\ $$
Commented by BaliramKumar last updated on 28/Jul/23

$$ \\ $$$$\frac{{x}^{\mathrm{2}} }{{cos}\mathrm{3}}\:+\:\frac{{y}^{\mathrm{2}} }{{sin}\mathrm{3}}\:=\:\mathrm{1} \\ $$$$\frac{{x}^{\mathrm{2}} }{−\mathrm{0}.\mathrm{98999}}\:+\:\frac{{y}^{\mathrm{2}} }{\mathrm{0}.\mathrm{14112}}\:=\:\mathrm{1} \\ $$$$\:\frac{{y}^{\mathrm{2}} }{\mathrm{0}.\mathrm{14112}}\:−\:\frac{{x}^{\mathrm{2}} }{\mathrm{0}.\mathrm{98999}}\:=\:\mathrm{1} \\ $$$${b}^{\mathrm{2}} \:=\:\mathrm{0}.\mathrm{14112},\:\:\:\:\:\:\:{a}^{\mathrm{2}} \:=\:\mathrm{0}.\mathrm{98999} \\ $$$${b}\:=\:\pm\sqrt{\mathrm{0}.\mathrm{14112}}\:\:\:,\:\:\:\:\:\:\:{a}\:=\:\pm\sqrt{\mathrm{0}.\mathrm{98999}} \\ $$$$ \\ $$$$\:\frac{{y}^{\mathrm{2}} }{\left(\pm\sqrt{\mathrm{0}.\mathrm{14112}}\right)^{\mathrm{2}} }\:−\:\frac{{x}^{\mathrm{2}} }{\left(\pm\sqrt{\mathrm{0}.\mathrm{98999}}\right)^{\mathrm{2}} }\:=\:\mathrm{1} \\ $$$$\:\frac{{y}^{\mathrm{2}} }{\left({b}\right)^{\mathrm{2}} }\:−\:\frac{{x}^{\mathrm{2}} }{\left({a}\right)^{\mathrm{2}} }\:=\:\mathrm{1} \\ $$$${hyperbolla} \\ $$
Commented by AST last updated on 28/Jul/23

$${cos}\left(\mathrm{3}°\right)\approx\mathrm{0}.\mathrm{9986} \\ $$$$\left(\frac{{x}}{{a}}\right)^{\mathrm{2}} +\left(\frac{{y}}{{b}}\right)^{\mathrm{2}} =\mathrm{1}\Rightarrow{x}={acos}\theta,{y}={bsin}\theta \\ $$$$\Rightarrow\left({x},{y}\right)=\left({acos}\theta,{bsin}\theta\right) \\ $$
Commented by AST last updated on 28/Jul/23

$${That}\:{would}\:{make}\:{a}\:{not}\:{real}. \\ $$
Commented by mr W last updated on 28/Jul/23

$${why}\:{does}\:{it}\:{make}\:{no}\:{real}\:{number}? \\ $$$$\mathrm{cos}\:\mathrm{3}=−{a}^{\mathrm{2}} \:{or}\:{a}=\sqrt{−\mathrm{cos}\:\mathrm{3}} \\ $$
Commented by AST last updated on 28/Jul/23

$${a}^{\mathrm{2}} ={cos}\mathrm{3}\Rightarrow{a}=\underset{−} {+}\sqrt{{cos}\:\mathrm{3}}\:{where}\:{cos}\mathrm{3}\:{is}\:−{ve}. \\ $$
Commented by mr W last updated on 28/Jul/23
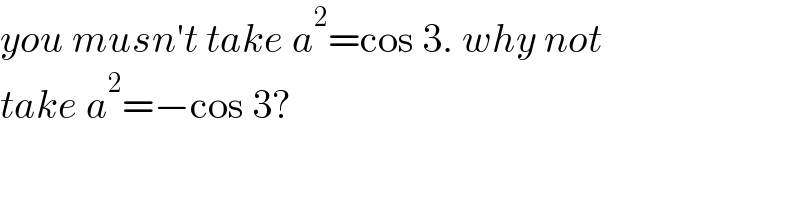
$${you}\:{musn}'{t}\:{take}\:{a}^{\mathrm{2}} =\mathrm{cos}\:\mathrm{3}.\:{why}\:{not} \\ $$$${take}\:{a}^{\mathrm{2}} =−\mathrm{cos}\:\mathrm{3}? \\ $$
Commented by AST last updated on 28/Jul/23

$$\frac{{x}^{\mathrm{2}} }{\:\left(\sqrt{{cos}\mathrm{3}}\right)^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{\left(\sqrt{{sin}\mathrm{3}}\right)^{\mathrm{2}} }=\mathrm{1}…\left({i}\right)\:\left({since}\:{cos}\mathrm{3},{sin}\mathrm{3}>\mathrm{0}\right) \\ $$$${Has}\:{the}\:{form}\:{of}\:{an}\:{ellipse}:\:\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}…\left({ii}\right) \\ $$$${By}\:{comparing}\:\left({i}\right)\:{and}\:\left({ii}\right),{we}\:{get}\:{a}^{\mathrm{2}} ={cos}\mathrm{3} \\ $$
Commented by mr W last updated on 28/Jul/23

Commented by AST last updated on 28/Jul/23

$${Hyperbola},\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{−{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${Let}\:{a}^{\mathrm{2}} ={cos}\mathrm{3}=−{p}^{\mathrm{2}} \:;{b}^{\mathrm{2}} ={sin}\mathrm{3}=−{q}^{\mathrm{2}} \left({where}\:{p}^{\mathrm{2}} ,{q}^{\mathrm{2}} >\mathrm{0}\right) \\ $$$${We}\:{get}\:\frac{{x}^{\mathrm{2}} }{−{p}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{q}^{\mathrm{2}} }=\frac{{y}^{\mathrm{2}} }{{q}^{\mathrm{2}} }−\frac{{x}^{\mathrm{2}} }{{p}^{\mathrm{2}} }=\mathrm{1}..\:{This}\:{gives}\:{a}\: \\ $$$${hyperbola}\:\left(\frac{{x}^{\mathrm{2}} }{{p}^{\mathrm{2}} }−\frac{{y}^{\mathrm{2}} }{{q}^{\mathrm{2}} }=\mathrm{1}\right)\:{rotated}\:{through}\:\mathrm{90}°\:{around} \\ $$$${the}\:{origin}. \\ $$$${We}\:{didn}'{t}\:{get}\:{this}\:{by}\:{taking}\:{a}^{\mathrm{2}} =−{cos}\mathrm{3} \\ $$$${but}\:{a}^{\mathrm{2}} ={cos}\mathrm{3}=−{p}^{\mathrm{2}} \\ $$
Commented by AST last updated on 28/Jul/23

$${When}\:{degrees}\:{are}\:{set}\:{as}\:{angular}\:{unit}\left({when}\:\mathrm{3}\right. \\ $$$$\left.{is}\:{measured}\:{in}\:{degrees}\right),{we}\:{get}\:{an}\:{ellipse}\:{as}\:{can} \\ $$$${be}\:{seen}\:{above}. \\ $$
Commented by AST last updated on 28/Jul/23

Commented by mr W last updated on 30/Jul/23

$${when}\:{normal}\:{earth}\:{people}\:{write}\: \\ $$$${sin}\:\mathrm{3}\:{or}\:\mathrm{cos}\:\mathrm{3},\:{they}\:{mean}\:\mathrm{3}\:{rad},\:{not} \\ $$$$\mathrm{3}\:{degrees}.\:{if}\:{they}\:{want}\:{to}\:{mean}\:\mathrm{3} \\ $$$${degrees},\:{they}\:{explictly}\:{write}\:\:\mathrm{sin}\:\mathrm{3}°\:{or} \\ $$$$\mathrm{cos}\:\mathrm{3}°.\:{this}\:{is}\:{a}\:{common}\:{convention}, \\ $$$${which}\:{normal}\:{earth}\:{people}\:{follow}: \\ $$
Commented by mr W last updated on 30/Jul/23

Commented by AST last updated on 30/Jul/23

$${The}\:{OP}\:{said}\:{it}\:{was}\:{in}\:{radians},\:{I}\:{was}\:{just} \\ $$$${considering}\:{the}\:{other}\:{possible}\:{case}.\:{I}\:{didn}'{t} \\ $$$${claim}\:{it}\:{was}\:{wrong}. \\ $$
Commented by AST last updated on 30/Jul/23

Commented by AST last updated on 30/Jul/23

$${Notations}\:{can}\:{vary}\:{depending}\:{on}\:{textbooks}, \\ $$$${countries},{etc}..\:{So},{there}\:{may}\:{not}\:{always}\:{be}\:{a} \\ $$$${fixed}\:{thing}\:{for}\:{the}\:{so}-{called}\:“{normal}\:{earth}'' \\ $$$${people}..\:{The}\:{OP}\:,{however},{later}\:{stated}\:{explicitly} \\ $$$${what}\:{he}\:{meant}. \\ $$
