Menu Close

Question-195484

Tinku Tara 0 Comments
Pin




Question Number 195484 by Shlock last updated on 03/Aug/23
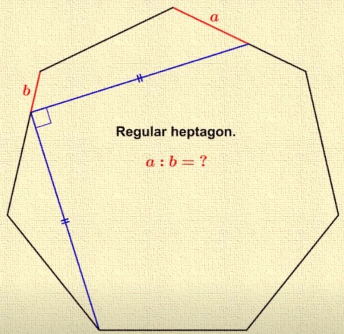
Answered by mr W last updated on 03/Aug/23
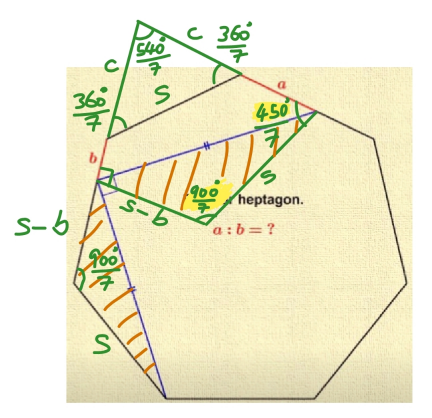
Commented by mr W last updated on 03/Aug/23
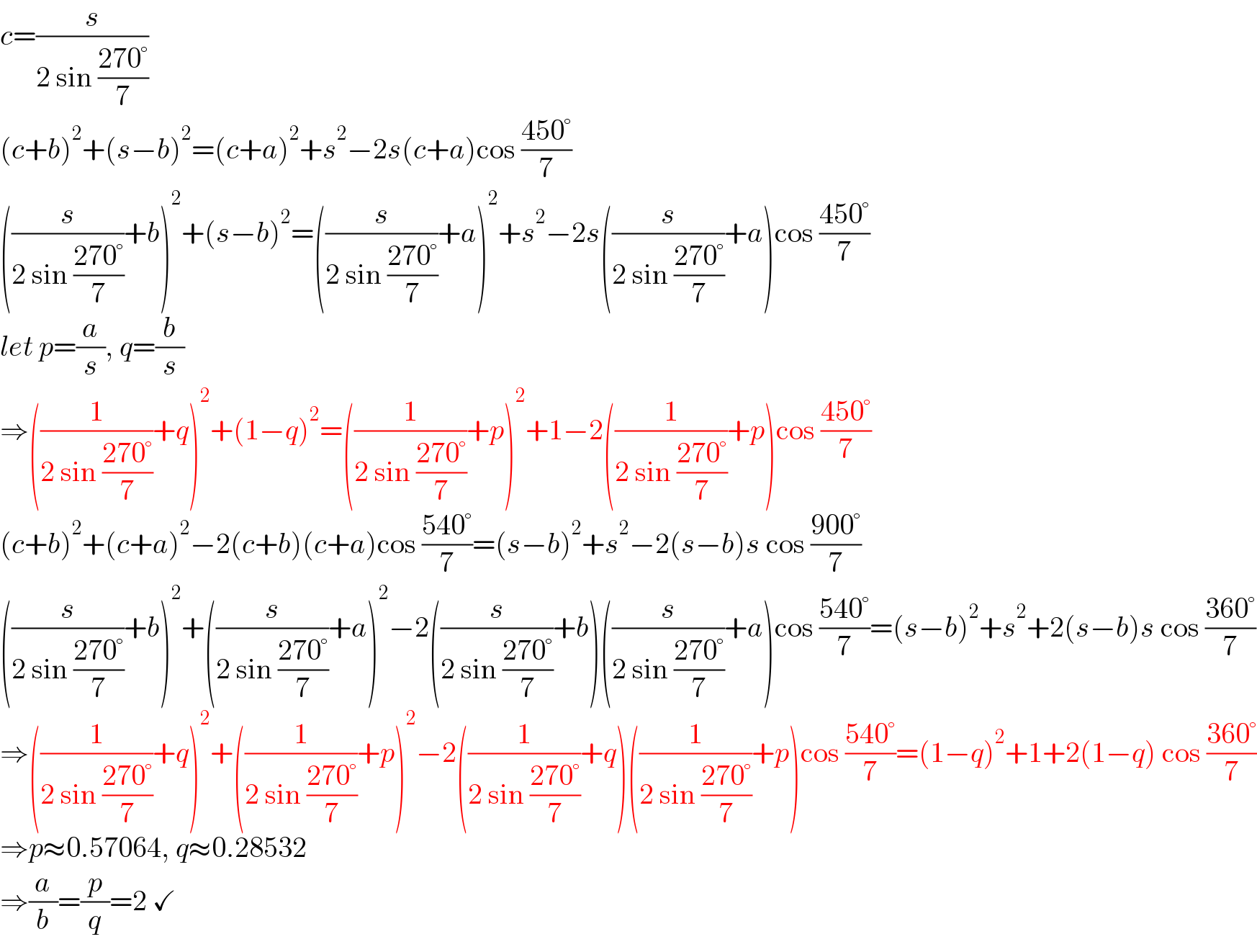
c=(s/(2 sin ((270°)/7))) (c+b)^2 +(s−b)^2 =(c+a)^2 +s^2 −2s(c+a)cos ((450°)/7) ((s/(2 sin ((270°)/7)))+b)^2 +(s−b)^2 =((s/(2 sin ((270°)/7)))+a)^2 +s^2 −2s((s/(2 sin ((270°)/7)))+a)cos ((450°)/7) let p=(a/s), q=(b/s) ⇒((1/(2 sin ((270°)/7)))+q)^2 +(1−q)^2 =((1/(2 sin ((270°)/7)))+p)^2 +1−2((1/(2 sin ((270°)/7)))+p)cos ((450°)/7) (c+b)^2 +(c+a)^2 −2(c+b)(c+a)cos ((540°)/7)=(s−b)^2 +s^2 −2(s−b)s cos ((900°)/7) ((s/(2 sin ((270°)/7)))+b)^2 +((s/(2 sin ((270°)/7)))+a)^2 −2((s/(2 sin ((270°)/7)))+b)((s/(2 sin ((270°)/7)))+a)cos ((540°)/7)=(s−b)^2 +s^2 +2(s−b)s cos ((360°)/7) ⇒((1/(2 sin ((270°)/7)))+q)^2 +((1/(2 sin ((270°)/7)))+p)^2 −2((1/(2 sin ((270°)/7)))+q)((1/(2 sin ((270°)/7)))+p)cos ((540°)/7)=(1−q)^2 +1+2(1−q) cos ((360°)/7) ⇒p≈0.57064, q≈0.28532 ⇒(a/b)=(p/q)=2 ✓
$${c}=\frac{{s}}{\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{270}°}{\mathrm{7}}} \\ $$$$\left({c}+{b}\right)^{\mathrm{2}} +\left({s}−{b}\right)^{\mathrm{2}} =\left({c}+{a}\right)^{\mathrm{2}} +{s}^{\mathrm{2}} −\mathrm{2}{s}\left({c}+{a}\right)\mathrm{cos}\:\frac{\mathrm{450}°}{\mathrm{7}} \\ $$$$\left(\frac{{s}}{\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{270}°}{\mathrm{7}}}+{b}\right)^{\mathrm{2}} +\left({s}−{b}\right)^{\mathrm{2}} =\left(\frac{{s}}{\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{270}°}{\mathrm{7}}}+{a}\right)^{\mathrm{2}} +{s}^{\mathrm{2}} −\mathrm{2}{s}\left(\frac{{s}}{\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{270}°}{\mathrm{7}}}+{a}\right)\mathrm{cos}\:\frac{\mathrm{450}°}{\mathrm{7}} \\ $$$${let}\:{p}=\frac{{a}}{{s}},\:{q}=\frac{{b}}{{s}} \\ $$$$\Rightarrow\left(\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{270}°}{\mathrm{7}}}+{q}\right)^{\mathrm{2}} +\left(\mathrm{1}−{q}\right)^{\mathrm{2}} =\left(\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{270}°}{\mathrm{7}}}+{p}\right)^{\mathrm{2}} +\mathrm{1}−\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{270}°}{\mathrm{7}}}+{p}\right)\mathrm{cos}\:\frac{\mathrm{450}°}{\mathrm{7}} \\ $$$$\left({c}+{b}\right)^{\mathrm{2}} +\left({c}+{a}\right)^{\mathrm{2}} −\mathrm{2}\left({c}+{b}\right)\left({c}+{a}\right)\mathrm{cos}\:\frac{\mathrm{540}°}{\mathrm{7}}=\left({s}−{b}\right)^{\mathrm{2}} +{s}^{\mathrm{2}} −\mathrm{2}\left({s}−{b}\right){s}\:\mathrm{cos}\:\frac{\mathrm{900}°}{\mathrm{7}} \\ $$$$\left(\frac{{s}}{\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{270}°}{\mathrm{7}}}+{b}\right)^{\mathrm{2}} +\left(\frac{{s}}{\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{270}°}{\mathrm{7}}}+{a}\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{{s}}{\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{270}°}{\mathrm{7}}}+{b}\right)\left(\frac{{s}}{\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{270}°}{\mathrm{7}}}+{a}\right)\mathrm{cos}\:\frac{\mathrm{540}°}{\mathrm{7}}=\left({s}−{b}\right)^{\mathrm{2}} +{s}^{\mathrm{2}} +\mathrm{2}\left({s}−{b}\right){s}\:\mathrm{cos}\:\frac{\mathrm{360}°}{\mathrm{7}} \\ $$$$\Rightarrow\left(\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{270}°}{\mathrm{7}}}+{q}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{270}°}{\mathrm{7}}}+{p}\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{270}°}{\mathrm{7}}}+{q}\right)\left(\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{270}°}{\mathrm{7}}}+{p}\right)\mathrm{cos}\:\frac{\mathrm{540}°}{\mathrm{7}}=\left(\mathrm{1}−{q}\right)^{\mathrm{2}} +\mathrm{1}+\mathrm{2}\left(\mathrm{1}−{q}\right)\:\mathrm{cos}\:\frac{\mathrm{360}°}{\mathrm{7}} \\ $$$$\Rightarrow{p}\approx\mathrm{0}.\mathrm{57064},\:{q}\approx\mathrm{0}.\mathrm{28532} \\ $$$$\Rightarrow\frac{{a}}{{b}}=\frac{{p}}{{q}}=\mathrm{2}\:\checkmark \\ $$
Commented by Shlock last updated on 03/Aug/23
Very great solution, Prof!

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *