Question Number 195570 by York12 last updated on 05/Aug/23
$$\mathrm{Given}\:\mathrm{three}\:\mathrm{Real}\:\mathrm{numbers}\:\left({x},{y},{z}\right),{such}\:{that} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} =\mathrm{1} \\ $$$${maximize} \\ $$$${x}^{\mathrm{4}} +{y}^{\mathrm{4}} −\mathrm{2}{z}^{\mathrm{4}} −\mathrm{3}\sqrt{\mathrm{2}}{xyz} \\ $$
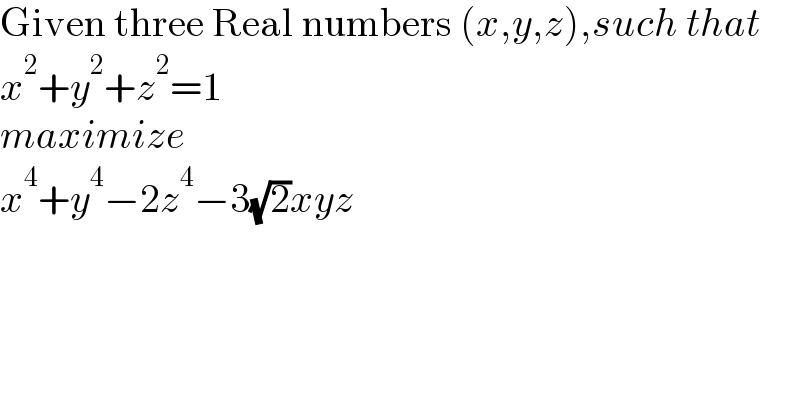
Commented by Frix last updated on 05/Aug/23
$$\mathrm{I}\:\mathrm{think}\:\mathrm{the}\:\mathrm{maximum}\:\mathrm{is}\:\frac{\mathrm{65}}{\mathrm{64}}\:\mathrm{when}\:{z}=\pm\frac{\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$
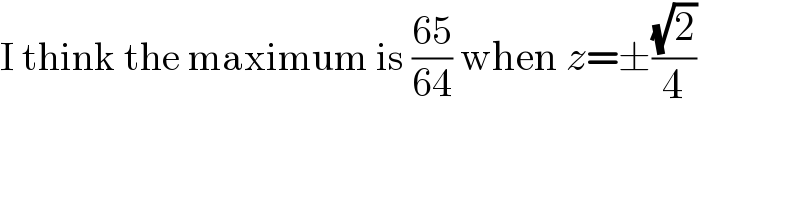
Commented by York12 last updated on 05/Aug/23
$${please}\:{provide}\:{workings} \\ $$
Answered by Frix last updated on 05/Aug/23
![x^2 +y^2 =1−z^2 ⇒ x^4 +y^4 =−2x^2 y^2 +z^4 −2z^2 +1 x^4 +y^4 −2z^4 −3(√2)xyz= =−2x^2 y^2 −3(√2)xyz−z^4 −2z^2 +1 Let t=xy −2t^2 −2(√2)tz−z^4 −2z^2 +1 ((d[−2t^2 −2(√2)tz−z^4 −2z^2 +1])/dt)=0 −4t−3(√2)z=0 ⇒ t=−((3(√2)z)/4) Inserting −z^4 +(z^2 /4)+1 ((d[−z^4 +(z^2 /4)+1])/dz)=0 −4z^3 +(z/2)=0 ⇒ z=±((√2)/4) [∨z=0_(minimum) ^(rejected because) ] ⇒ maximum is ((65)/(64)) ★ We have z=((√2)/4)∧xy=−(3/8) ∨ z=−((√2)/4)∧xy=(3/8) x^2 +y^2 =1−z^2 =(7/8) The values are easy to calculate](https://www.tinkutara.com/question/Q195599.png)
$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1}−{z}^{\mathrm{2}} \:\Rightarrow\:{x}^{\mathrm{4}} +{y}^{\mathrm{4}} =−\mathrm{2}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{z}^{\mathrm{4}} −\mathrm{2}{z}^{\mathrm{2}} +\mathrm{1} \\ $$$$ \\ $$$${x}^{\mathrm{4}} +{y}^{\mathrm{4}} −\mathrm{2}{z}^{\mathrm{4}} −\mathrm{3}\sqrt{\mathrm{2}}{xyz}= \\ $$$$=−\mathrm{2}{x}^{\mathrm{2}} {y}^{\mathrm{2}} −\mathrm{3}\sqrt{\mathrm{2}}{xyz}−{z}^{\mathrm{4}} −\mathrm{2}{z}^{\mathrm{2}} +\mathrm{1} \\ $$$$\mathrm{Let}\:{t}={xy} \\ $$$$−\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{2}}{tz}−{z}^{\mathrm{4}} −\mathrm{2}{z}^{\mathrm{2}} +\mathrm{1} \\ $$$$\frac{{d}\left[−\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{2}}{tz}−{z}^{\mathrm{4}} −\mathrm{2}{z}^{\mathrm{2}} +\mathrm{1}\right]}{{dt}}=\mathrm{0} \\ $$$$−\mathrm{4}{t}−\mathrm{3}\sqrt{\mathrm{2}}{z}=\mathrm{0}\:\Rightarrow\:{t}=−\frac{\mathrm{3}\sqrt{\mathrm{2}}{z}}{\mathrm{4}} \\ $$$$\mathrm{Inserting} \\ $$$$−{z}^{\mathrm{4}} +\frac{{z}^{\mathrm{2}} }{\mathrm{4}}+\mathrm{1} \\ $$$$\frac{{d}\left[−{z}^{\mathrm{4}} +\frac{{z}^{\mathrm{2}} }{\mathrm{4}}+\mathrm{1}\right]}{{dz}}=\mathrm{0} \\ $$$$−\mathrm{4}{z}^{\mathrm{3}} +\frac{{z}}{\mathrm{2}}=\mathrm{0}\:\Rightarrow\:{z}=\pm\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\:\left[\vee{z}=\mathrm{0}_{\mathrm{minimum}} ^{\mathrm{rejected}\:\mathrm{because}} \right] \\ $$$$\Rightarrow\:\mathrm{maximum}\:\mathrm{is}\:\frac{\mathrm{65}}{\mathrm{64}}\:\bigstar \\ $$$$\mathrm{We}\:\mathrm{have} \\ $$$$\mathrm{z}=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\wedge{xy}=−\frac{\mathrm{3}}{\mathrm{8}}\:\vee\:{z}=−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\wedge{xy}=\frac{\mathrm{3}}{\mathrm{8}} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1}−{z}^{\mathrm{2}} =\frac{\mathrm{7}}{\mathrm{8}} \\ $$$$\mathrm{The}\:\mathrm{values}\:\mathrm{are}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{calculate} \\ $$
Commented by York12 last updated on 05/Aug/23
$${ORZ} \\ $$$$ \\ $$$$ \\ $$
Commented by York12 last updated on 05/Aug/23
$${where}\:{to}\:{learn}\:{inequalities}\: \\ $$$${and}\:{are}\:{you}\:{using}\:{discord}\: \\ $$$${I}\:{would}\:{like}\:{to}\:{invite}\:{you}\:{to}\:{our}\:{community} \\ $$$$ \\ $$
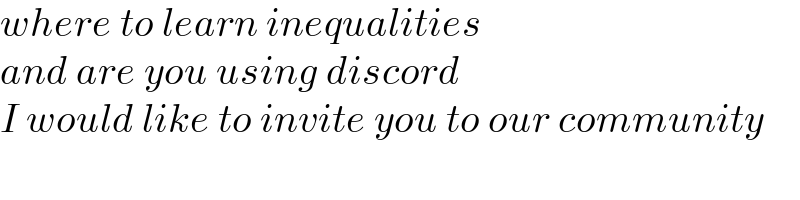
Commented by Frix last updated on 05/Aug/23
Sorry I don't use any social media platforms.
I studied mathematics & physics decades ago at a university, I don't know where else you could learn these things.
Commented by York12 last updated on 05/Aug/23
$${okay}\:{sir}\:{thanks} \\ $$
Commented by York12 last updated on 05/Aug/23
$${but}\:{if}\:{you}\:{wanted}\:{you}\:{are}\:{always}\:{welcome} \\ $$$${we}\:{are}\:{a}\:{big}\:{community}\:{of}\:{high}\:{scholars} \\ $$$${from}\:{different}\:{spots}\:{on}\:{the}\:{earth}\:{and}\:{we} \\ $$$${need}\:{instructions}\:{from}\:{an}\:{efficient} \\ $$$${person}\:{like}\:{you}\:{sir} \\ $$
Commented by necx122 last updated on 06/Aug/23
$${you}\:{could}\:{share}\:{the}\:{link},\:{a}\:{few}\:{of}\:{us}\:{are} \\ $$$${also}\:{interested}. \\ $$
Commented by York12 last updated on 06/Aug/23
$${great} \\ $$
Commented by York12 last updated on 06/Aug/23
$$ \\ $$https://discord.gg/mods