Question Number 195611 by Mingma last updated on 05/Aug/23
Answered by mr W last updated on 06/Aug/23

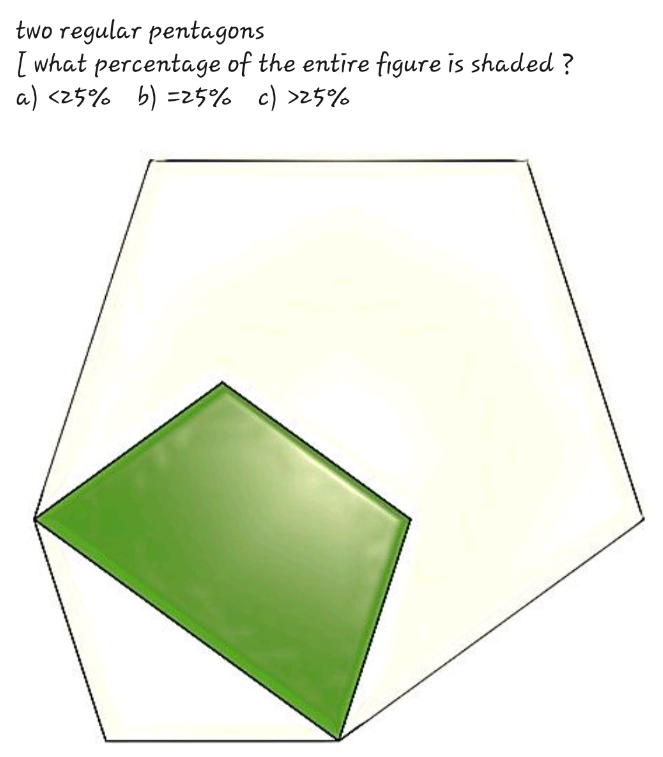
$${a}={side}\:{length}\:{of}\:{small}\:{pentagon} \\ $$$${b}={side}\:{length}\:{of}\:{big}\:{pentagon} \\ $$$${b}=\mathrm{2}{a}\:\mathrm{sin}\:\mathrm{54}° \\ $$$${a}=\mathrm{2}{r}\:\mathrm{sin}\:\mathrm{36}°\:\Rightarrow{r}=\frac{{a}}{\mathrm{2}\:\mathrm{sin}\:\mathrm{36}°} \\ $$$${b}=\mathrm{2}{R}\:\mathrm{sin}\:\mathrm{36}°\:\Rightarrow{R}=\frac{{b}}{\mathrm{2}\:\mathrm{sin}\:\mathrm{36}°}=\frac{{a}\:\mathrm{sin}\:\mathrm{54}°}{\mathrm{sin}\:\mathrm{36}°} \\ $$$${total}\:{area}\:=\frac{\mathrm{5}\:{R}^{\mathrm{2}} \:\mathrm{sin}\:\mathrm{72}°}{\mathrm{2}}+\frac{{a}^{\mathrm{2}} \mathrm{sin}\:\mathrm{72}°}{\mathrm{2}} \\ $$$${shaded}\:{area}=\frac{\mathrm{5}\:{r}^{\mathrm{2}} \:\mathrm{sin}\:\mathrm{72}°}{\mathrm{2}}−\frac{{a}^{\mathrm{2}} \mathrm{sin}\:\mathrm{72}°}{\mathrm{2}} \\ $$$$\frac{{shaded}}{{total}}=\frac{\mathrm{5}{r}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{5}{R}^{\mathrm{2}} +{a}^{\mathrm{2}} }=\frac{\mathrm{5}\left(\frac{{r}}{{a}}\right)^{\mathrm{2}} −\mathrm{1}}{\mathrm{5}\left(\frac{{R}}{{a}}\right)^{\mathrm{2}} +\mathrm{1}} \\ $$$$\:\:=\frac{\mathrm{5}\left(\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\mathrm{36}°}\right)^{\mathrm{2}} −\mathrm{1}}{\mathrm{5}\left(\frac{\mathrm{sin}\:\mathrm{54}°}{\mathrm{sin}\:\mathrm{36}°}\right)^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{25\%} \\ $$$$\left.\Rightarrow{answer}\:{b}\right) \\ $$
Commented by Mingma last updated on 06/Aug/23
Perfect ��
