Menu Close

Prove-that-n-N-n-1-n-lnt-dt-ln-n-1-n-t-dt-

Tinku Tara 0 Comments
Pin




Question Number 196522 by Erico last updated on 26/Aug/23
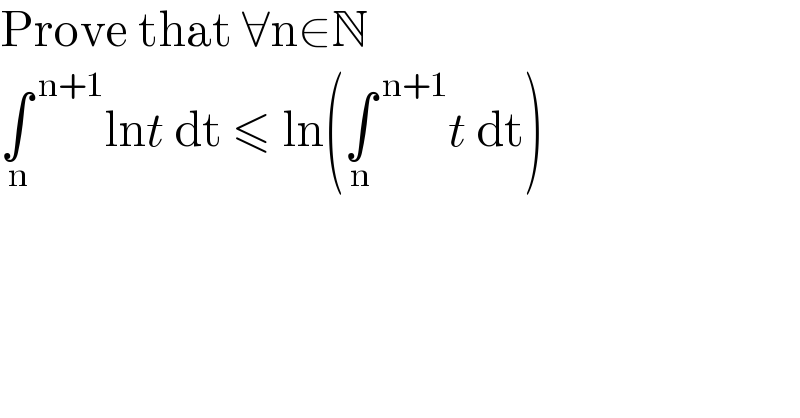
Prove that ∀n∈N ∫^( n+1) _( n) lnt dt ≤ ln(∫^( n+1) _n t dt)
$$\mathrm{Prove}\:\mathrm{that}\:\forall\mathrm{n}\in\mathbb{N} \\ $$$$\underset{\:\mathrm{n}} {\int}^{\:\mathrm{n}+\mathrm{1}} \mathrm{ln}{t}\:\mathrm{dt}\:\leqslant\:\mathrm{ln}\left(\underset{\mathrm{n}} {\int}^{\:\mathrm{n}+\mathrm{1}} {t}\:\mathrm{dt}\right) \\ $$
Answered by aleks041103 last updated on 26/Aug/23
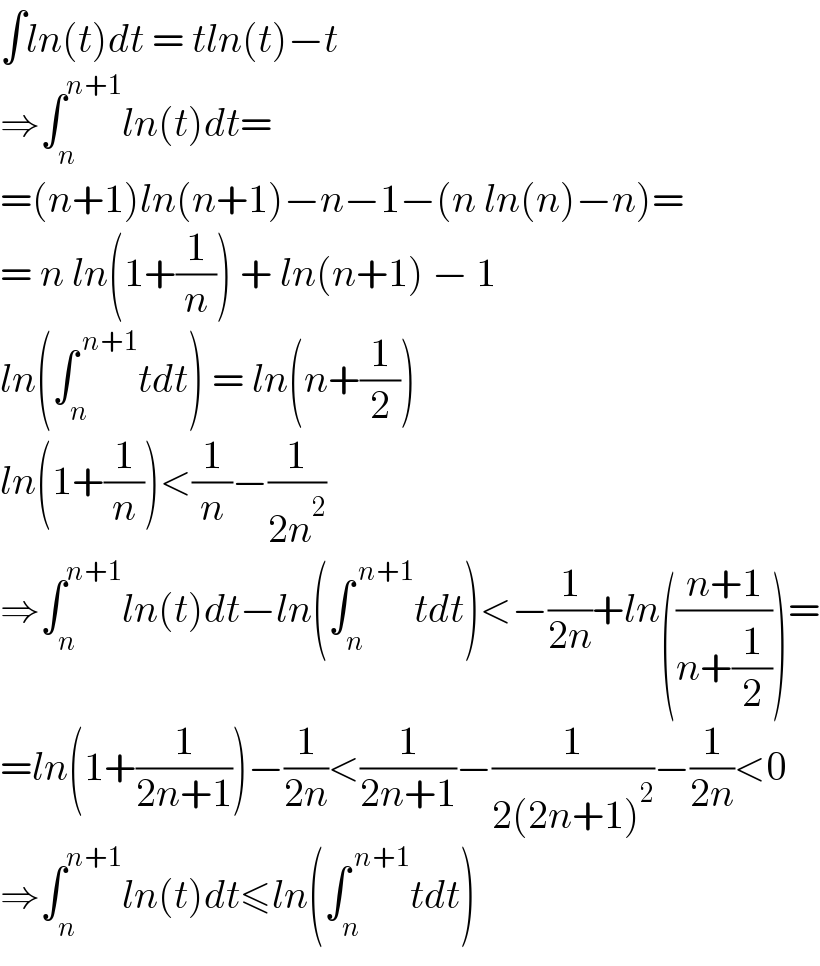
∫ln(t)dt = tln(t)−t ⇒∫_n ^(n+1) ln(t)dt= =(n+1)ln(n+1)−n−1−(n ln(n)−n)= = n ln(1+(1/n)) + ln(n+1) − 1 ln(∫_n ^( n+1) tdt) = ln(n+(1/2)) ln(1+(1/n))<(1/n)−(1/(2n^2 )) ⇒∫_n ^(n+1) ln(t)dt−ln(∫_n ^( n+1) tdt)<−(1/(2n))+ln(((n+1)/(n+(1/2))))= =ln(1+(1/(2n+1)))−(1/(2n))<(1/(2n+1))−(1/(2(2n+1)^2 ))−(1/(2n))<0 ⇒∫_n ^(n+1) ln(t)dt≤ln(∫_n ^( n+1) tdt)
$$\int{ln}\left({t}\right){dt}\:=\:{tln}\left({t}\right)−{t} \\ $$$$\Rightarrow\int_{{n}} ^{{n}+\mathrm{1}} {ln}\left({t}\right){dt}= \\ $$$$=\left({n}+\mathrm{1}\right){ln}\left({n}+\mathrm{1}\right)−{n}−\mathrm{1}−\left({n}\:{ln}\left({n}\right)−{n}\right)= \\ $$$$=\:{n}\:{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)\:+\:{ln}\left({n}+\mathrm{1}\right)\:−\:\mathrm{1} \\ $$$${ln}\left(\int_{{n}} ^{\:{n}+\mathrm{1}} {tdt}\right)\:=\:{ln}\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)<\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} } \\ $$$$\Rightarrow\int_{{n}} ^{{n}+\mathrm{1}} {ln}\left({t}\right){dt}−{ln}\left(\int_{{n}} ^{\:{n}+\mathrm{1}} {tdt}\right)<−\frac{\mathrm{1}}{\mathrm{2}{n}}+{ln}\left(\frac{{n}+\mathrm{1}}{{n}+\frac{\mathrm{1}}{\mathrm{2}}}\right)= \\ $$$$={ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right)−\frac{\mathrm{1}}{\mathrm{2}{n}}<\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}{n}}<\mathrm{0} \\ $$$$\Rightarrow\int_{{n}} ^{{n}+\mathrm{1}} {ln}\left({t}\right){dt}\leqslant{ln}\left(\int_{{n}} ^{\:{n}+\mathrm{1}} {tdt}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *