Menu Close

Question-196493

Tinku Tara 0 Comments
Pin




Question Number 196493 by mr W last updated on 26/Aug/23
Commented by mr W last updated on 27/Aug/23
solution to question #196172
$${solution}\:{to}\:{question}\:#\mathrm{196172} \\ $$
Answered by mr W last updated on 29/Aug/23
U_k sin φ_k t_k −((g cos θ)/2)t_k ^2 =0 ⇒t_k =((2U_k sin φ_k )/(g cos θ)) s_k =U_k cos φ_k t_k +((g sin θ)/2)t_k ^2 s_k =U_k cos φ_k ×((2U_k sin φ_k )/(g cos θ))+((g sin θ)/2)×(((2U_k sin φ_k )/(g cos θ)))^2 ⇒s_k =((2U_k ^2 )/(g cos θ))×(((1/(tan φ_k ))+tan θ)/(1+(1/(tan^2 φ_k )))) V_(kx) =U_k cos φ_k +g sin θ t_k V_(kx) =U_k cos φ_k +g sin θ×((2U_k sin φ_k )/(g cos θ)) ⇒V_(kx) =U_k sin φ_k ((1/(tan φ_k ))+2 tan θ) V_(ky) =U_k sin φ_k −g cos θ×t_k V_(ky) =U_k sin φ_k −g cos θ×((2U_k sin φ_k )/(g cos θ)) ⇒V_(ky) =−U_k sin φ_k U_(k+1) cos φ_(k+1) =V_(kx) ⇒U_(k+1) cos φ_(k+1) =U_k sin φ_k ((1/(tan φ_k ))+2 tan θ) U_(k+1) sin φ_(k+1) =−eV_(ky) ⇒U_(k+1) sin φ_(k+1) =eU_k sin φ_k ⇒(1/(tan φ_(k+1) ))=(1/e)((1/(tan φ_k ))+2 tan θ) (U_(k+1) /U_k )=((e sin φ_k )/(sin φ_(k+1) )) (U_(k+1) ^2 /U_k ^2 )=((e^2 (1+(1/(tan^2 φ_(k+1) ))))/(1+(1/(tan^2 φ_k )))) ⇒(U_(k+1) ^2 /U_k ^2 )=((e^2 +((1/(tan φ_k ))+2 tan θ)^2 )/(1+(1/(tan^2 φ_k )))) let δ_k =(1/(tan φ_k )) s_k =((2U_k ^2 )/(g cos θ))×((δ_k +tan θ)/(1+δ_k ^2 )) U_(k+1) =U_k (√((e^2 +(δ_k +2 tan θ)^2 )/(1+δ_k ^2 ))) δ_(k+1) =(1/e)(δ_k +2 tan θ) U_1 =u φ_1 =π−ϕ δ_1 =(1/(tan φ_1 ))=−(1/(tan ϕ))=λ such that the ball exactly returns to the start point, s_1 +s_2 +s_3 +...+s_n =0 from which we can get λ, thus φ_1 ,φ_2 ... some examples for n=3 and 4:
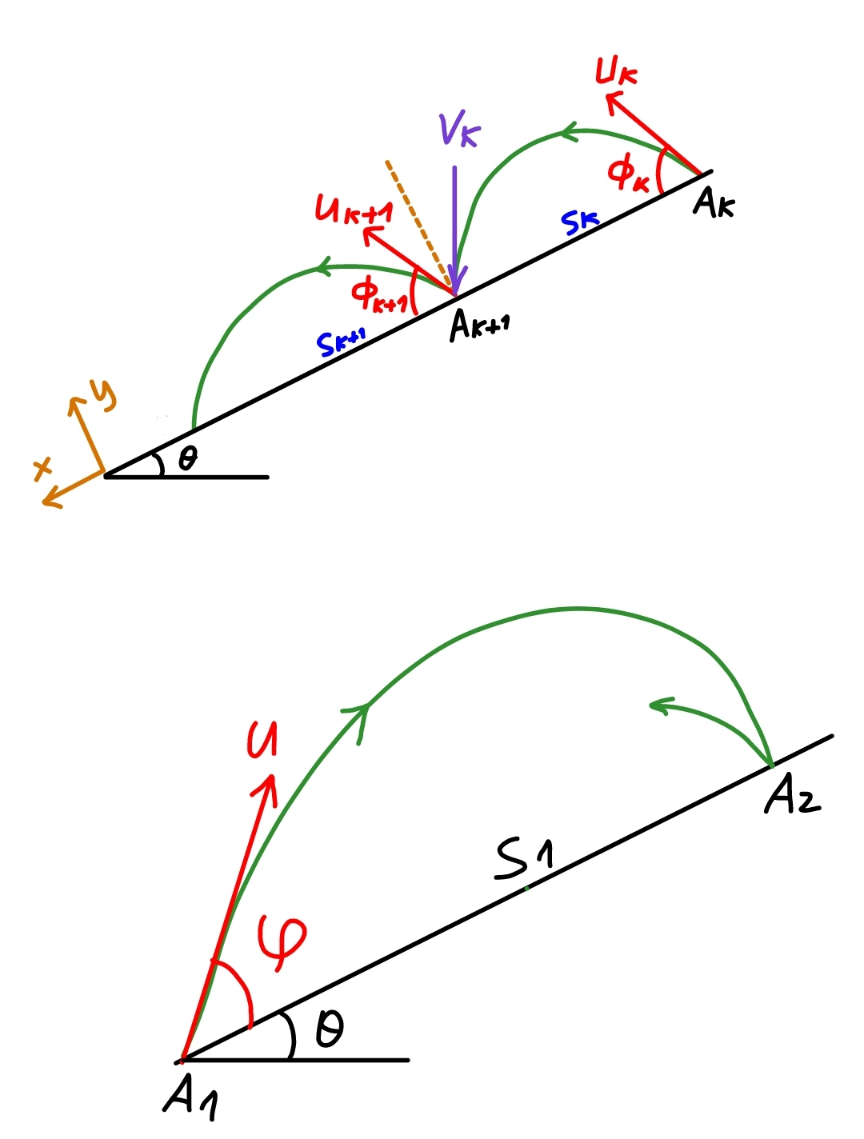
$${U}_{{k}} \mathrm{sin}\:\phi_{{k}} {t}_{{k}} −\frac{{g}\:\mathrm{cos}\:\theta}{\mathrm{2}}{t}_{{k}} ^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{t}_{{k}} =\frac{\mathrm{2}{U}_{{k}} \:\mathrm{sin}\:\phi_{{k}} }{{g}\:\mathrm{cos}\:\theta} \\ $$$${s}_{{k}} ={U}_{{k}} \mathrm{cos}\:\phi_{{k}} {t}_{{k}} +\frac{{g}\:\mathrm{sin}\:\theta}{\mathrm{2}}{t}_{{k}} ^{\mathrm{2}} \\ $$$${s}_{{k}} ={U}_{{k}} \mathrm{cos}\:\phi_{{k}} ×\frac{\mathrm{2}{U}_{{k}} \:\mathrm{sin}\:\phi_{{k}} }{{g}\:\mathrm{cos}\:\theta}+\frac{{g}\:\mathrm{sin}\:\theta}{\mathrm{2}}×\left(\frac{\mathrm{2}{U}_{{k}} \:\mathrm{sin}\:\phi_{{k}} }{{g}\:\mathrm{cos}\:\theta}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{s}_{{k}} =\frac{\mathrm{2}{U}_{{k}} ^{\mathrm{2}} }{{g}\:\mathrm{cos}\:\theta}×\frac{\frac{\mathrm{1}}{\mathrm{tan}\:\phi_{{k}} }+\mathrm{tan}\:\theta}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{2}} \:\phi_{{k}} }} \\ $$$${V}_{{kx}} ={U}_{{k}} \mathrm{cos}\:\phi_{{k}} +{g}\:\mathrm{sin}\:\theta\:{t}_{{k}} \\ $$$${V}_{{kx}} ={U}_{{k}} \mathrm{cos}\:\phi_{{k}} +{g}\:\mathrm{sin}\:\theta×\frac{\mathrm{2}{U}_{{k}} \:\mathrm{sin}\:\phi_{{k}} }{{g}\:\mathrm{cos}\:\theta} \\ $$$$\Rightarrow{V}_{{kx}} ={U}_{{k}} \mathrm{sin}\:\phi_{{k}} \left(\frac{\mathrm{1}}{\mathrm{tan}\:\phi_{{k}} }+\mathrm{2}\:\mathrm{tan}\:\theta\right) \\ $$$${V}_{{ky}} ={U}_{{k}} \mathrm{sin}\:\phi_{{k}} −{g}\:\mathrm{cos}\:\theta×{t}_{{k}} \\ $$$${V}_{{ky}} ={U}_{{k}} \mathrm{sin}\:\phi_{{k}} −{g}\:\mathrm{cos}\:\theta×\frac{\mathrm{2}{U}_{{k}} \:\mathrm{sin}\:\phi_{{k}} }{{g}\:\mathrm{cos}\:\theta} \\ $$$$\Rightarrow{V}_{{ky}} =−{U}_{{k}} \mathrm{sin}\:\phi_{{k}} \\ $$$${U}_{{k}+\mathrm{1}} \mathrm{cos}\:\phi_{{k}+\mathrm{1}} ={V}_{{kx}} \\ $$$$\Rightarrow{U}_{{k}+\mathrm{1}} \mathrm{cos}\:\phi_{{k}+\mathrm{1}} ={U}_{{k}} \mathrm{sin}\:\phi_{{k}} \left(\frac{\mathrm{1}}{\mathrm{tan}\:\phi_{{k}} }+\mathrm{2}\:\mathrm{tan}\:\theta\right) \\ $$$${U}_{{k}+\mathrm{1}} \mathrm{sin}\:\phi_{{k}+\mathrm{1}} =−{eV}_{{ky}} \\ $$$$\Rightarrow{U}_{{k}+\mathrm{1}} \mathrm{sin}\:\phi_{{k}+\mathrm{1}} ={eU}_{{k}} \mathrm{sin}\:\phi_{{k}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{tan}\:\phi_{{k}+\mathrm{1}} }=\frac{\mathrm{1}}{{e}}\left(\frac{\mathrm{1}}{\mathrm{tan}\:\phi_{{k}} }+\mathrm{2}\:\mathrm{tan}\:\theta\right) \\ $$$$\frac{{U}_{{k}+\mathrm{1}} }{{U}_{{k}} }=\frac{{e}\:\mathrm{sin}\:\phi_{{k}} }{\mathrm{sin}\:\phi_{{k}+\mathrm{1}} } \\ $$$$\frac{{U}_{{k}+\mathrm{1}} ^{\mathrm{2}} }{{U}_{{k}} ^{\mathrm{2}} }=\frac{{e}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{2}} \:\phi_{{k}+\mathrm{1}} }\right)}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{2}} \:\phi_{{k}} }} \\ $$$$\Rightarrow\frac{{U}_{{k}+\mathrm{1}} ^{\mathrm{2}} }{{U}_{{k}} ^{\mathrm{2}} }=\frac{{e}^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{tan}\:\phi_{{k}} }+\mathrm{2}\:\mathrm{tan}\:\theta\right)^{\mathrm{2}} }{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{2}} \:\phi_{{k}} }} \\ $$$${let}\:\delta_{{k}} =\frac{\mathrm{1}}{\mathrm{tan}\:\phi_{{k}} } \\ $$$${s}_{{k}} =\frac{\mathrm{2}{U}_{{k}} ^{\mathrm{2}} }{{g}\:\mathrm{cos}\:\theta}×\frac{\delta_{{k}} +\mathrm{tan}\:\theta}{\mathrm{1}+\delta_{{k}} ^{\mathrm{2}} } \\ $$$${U}_{{k}+\mathrm{1}} ={U}_{{k}} \sqrt{\frac{{e}^{\mathrm{2}} +\left(\delta_{{k}} +\mathrm{2}\:\mathrm{tan}\:\theta\right)^{\mathrm{2}} }{\mathrm{1}+\delta_{{k}} ^{\mathrm{2}} }} \\ $$$$\delta_{{k}+\mathrm{1}} =\frac{\mathrm{1}}{{e}}\left(\delta_{{k}} +\mathrm{2}\:\mathrm{tan}\:\theta\right) \\ $$$${U}_{\mathrm{1}} ={u} \\ $$$$\phi_{\mathrm{1}} =\pi−\varphi \\ $$$$\delta_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{tan}\:\phi_{\mathrm{1}} }=−\frac{\mathrm{1}}{\mathrm{tan}\:\varphi}=\lambda \\ $$$${such}\:{that}\:{the}\:{ball}\:{exactly}\:{returns}\:{to} \\ $$$${the}\:{start}\:{point}, \\ $$$${s}_{\mathrm{1}} +{s}_{\mathrm{2}} +{s}_{\mathrm{3}} +…+{s}_{{n}} =\mathrm{0} \\ $$$${from}\:{which}\:{we}\:{can}\:{get}\:\lambda,\:{thus}\:\phi_{\mathrm{1}} ,\phi_{\mathrm{2}} … \\ $$$${some}\:{examples}\:{for}\:{n}=\mathrm{3}\:{and}\:\mathrm{4}: \\ $$
Commented by mr W last updated on 27/Aug/23
Commented by mr W last updated on 26/Aug/23
Commented by mr W last updated on 26/Aug/23
Commented by mr W last updated on 26/Aug/23
Commented by mr W last updated on 27/Aug/23
Commented by mr W last updated on 28/Aug/23
δ_(k+1) =(1/e)(δ_k +2 tan θ) say δ_(k+1) +A=(1/e)(δ_k +A) δ_(k+1) =(1/e)[δ_k +(1−e)A] (1−e)A=2 tan θ ⇒A=((2 tan θ)/(1−e)) δ_(k+1) +((2 tan θ)/(1−e))=(1/e)(δ_k +((2 tan θ)/(1−e))) ⇒δ_k +((2 tan θ)/(1−e))=(1/e^(k−1) )(δ_1 +((2 tan θ)/(1−e))) determinant ((((1/(tan φ_k ))=(1/e^(k−1) )(−(1/(tan ϕ))+((2 tan θ)/(1−e)))−((2 tan θ)/(1−e)))))
$$\delta_{{k}+\mathrm{1}} =\frac{\mathrm{1}}{{e}}\left(\delta_{{k}} +\mathrm{2}\:\mathrm{tan}\:\theta\right) \\ $$$${say}\:\delta_{{k}+\mathrm{1}} +{A}=\frac{\mathrm{1}}{{e}}\left(\delta_{{k}} +{A}\right) \\ $$$$\delta_{{k}+\mathrm{1}} =\frac{\mathrm{1}}{{e}}\left[\delta_{{k}} +\left(\mathrm{1}−{e}\right){A}\right] \\ $$$$\left(\mathrm{1}−{e}\right){A}=\mathrm{2}\:\mathrm{tan}\:\theta \\ $$$$\Rightarrow{A}=\frac{\mathrm{2}\:\mathrm{tan}\:\theta}{\mathrm{1}−{e}} \\ $$$$\delta_{{k}+\mathrm{1}} +\frac{\mathrm{2}\:\mathrm{tan}\:\theta}{\mathrm{1}−{e}}=\frac{\mathrm{1}}{{e}}\left(\delta_{{k}} +\frac{\mathrm{2}\:\mathrm{tan}\:\theta}{\mathrm{1}−{e}}\right) \\ $$$$\Rightarrow\delta_{{k}} +\frac{\mathrm{2}\:\mathrm{tan}\:\theta}{\mathrm{1}−{e}}=\frac{\mathrm{1}}{{e}^{{k}−\mathrm{1}} }\left(\delta_{\mathrm{1}} +\frac{\mathrm{2}\:\mathrm{tan}\:\theta}{\mathrm{1}−{e}}\right) \\ $$$$\begin{array}{|c|}{\frac{\mathrm{1}}{\mathrm{tan}\:\phi_{{k}} }=\frac{\mathrm{1}}{{e}^{{k}−\mathrm{1}} }\left(−\frac{\mathrm{1}}{\mathrm{tan}\:\varphi}+\frac{\mathrm{2}\:\mathrm{tan}\:\theta}{\mathrm{1}−{e}}\right)−\frac{\mathrm{2}\:\mathrm{tan}\:\theta}{\mathrm{1}−{e}}}\\\hline\end{array} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *